Graphing Conic Sections Part 4: Hyperbolas
Summary
TLDRProfessor Dave explains the concept of hyperbolas, the final conic section in geometry. A hyperbola consists of two branches that are defined by the constant difference of distances to two foci. The equation for a hyperbola is similar to that of an ellipse, with the key difference being a minus sign instead of a plus. The professor covers important aspects such as vertices, foci, asymptotes, and how to graph a hyperbola. He also shows how to generate the equation from given vertices and foci coordinates, and how transformations affect the graph.
Takeaways
- 📈 A hyperbola is a conic section formed when a plane cuts through both halves of a double cone, creating two separate curved branches.
- 🔍 The definition of a hyperbola involves two foci, where the constant difference of distances from any point on the hyperbola to the foci is maintained.
- 🎯 The foci are located outside the branches, while the vertices lie between them, connected by the transverse axis that also contains the center.
- ➕ The hyperbola’s equation resembles that of an ellipse, but uses a subtraction sign instead of addition, reflecting the constant difference property.
- ↔️ If the x-term comes first in the equation, the hyperbola opens along the x-axis; if the y-term comes first, it opens along the y-axis.
- 📏 The parameter 'a' represents the distance from the center to each vertex, while 'c' is the distance from the center to each focus.
- 📐 For hyperbolas, the relationship between the parameters is given by c² = a² + b², differing from ellipses where c² = a² - b².
- 🧮 When given an equation, values for a, b, and c can determine the positions of vertices and foci, helping to sketch the hyperbola.
- 📊 Asymptotes help guide the shape of the hyperbola and are represented by y = (b/a)x and y = -(b/a)x for horizontal hyperbolas, or y = (a/b)x and y = -(a/b)x for vertical ones.
- 🔄 Hyperbolas can be translated from the origin by replacing x and y with (x - h) and (y - k), making (h, k) the new center.
- 🧭 When the hyperbola’s equation is not in standard form, dividing by the leading coefficient normalizes it for easier graphing.
Q & A
What is a hyperbola in geometry?
-A hyperbola is a conic section formed when a plane cuts through both halves of a double cone. It consists of two separate curves, called branches, that open in opposite directions.
How does the definition of a hyperbola differ from that of an ellipse?
-While an ellipse consists of all points whose total distance to two foci is constant, a hyperbola consists of all points whose absolute difference in distances to two foci is constant.
What are the key parts of a hyperbola?
-The main components are the center, vertices, foci, transverse axis, and asymptotes. The branches of the hyperbola extend outward from the vertices along the transverse axis.
How is the standard equation of a hyperbola different from that of an ellipse?
-The equations are similar except that the ellipse has a plus sign between the squared terms, while the hyperbola has a minus sign, reflecting the difference-based definition of the hyperbola.
What determines whether a hyperbola opens horizontally or vertically?
-If the x-term appears first in the equation, the hyperbola opens horizontally around the x-axis. If the y-term appears first, it opens vertically around the y-axis.
What do the parameters a, b, and c represent in a hyperbola?
-‘a’ is the distance from the center to each vertex, ‘c’ is the distance from the center to each focus, and ‘b’ is used algebraically to relate a and c using the formula c² = a² + b².
How do you find the coordinates of the vertices and foci from a hyperbola’s equation?
-If the equation is in standard form, the vertices are located at ±a from the center along the transverse axis, and the foci are located at ±c along the same axis.
What are asymptotes in a hyperbola and why are they important?
-Asymptotes are diagonal lines that the hyperbola’s branches approach but never touch. They help in sketching accurate graphs of hyperbolas by guiding the curvature of each branch.
What are the equations of the asymptotes for a hyperbola?
-For a hyperbola opening along the x-axis, the asymptotes are y = ±(b/a)x. For one opening along the y-axis, they are y = ±(a/b)x.
How can a hyperbola be shifted from the origin to a new center point?
-By replacing x and y with (x – h) and (y – k) in the standard equation, the hyperbola’s center moves to the point (h, k).
What is the process for putting a non-standard hyperbola equation into standard form?
-If the equation has a constant other than 1 on the right-hand side, divide all terms by that constant so the right-hand side becomes 1, placing the equation in standard form.
How can you determine the equation of a hyperbola from given vertices and foci?
-Use the vertex distance to find a², the focus distance to find c², and apply the relation c² = a² + b² to solve for b². Then plug a² and b² into the standard hyperbola equation, choosing the correct orientation based on the axis.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Intro to Conic Sections | Pre Calculus | STEM Math
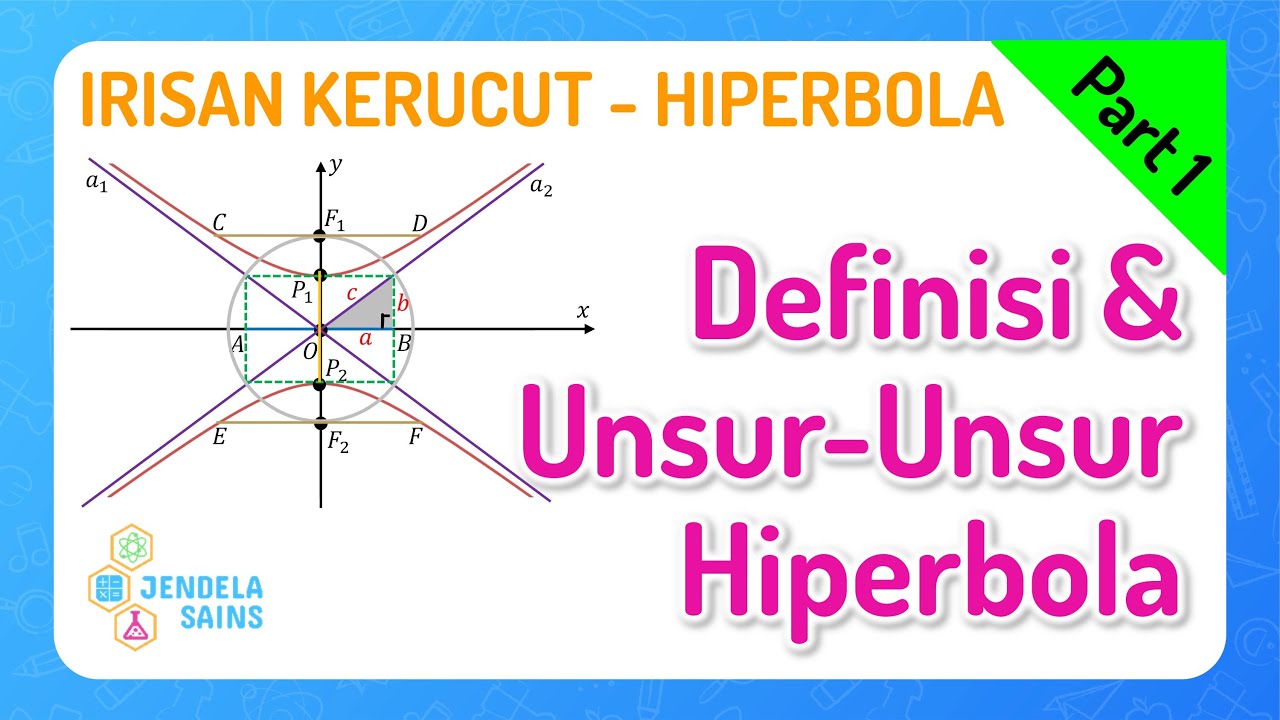
Irisan Kerucut - Hiperbola • Part 1: Definisi dan Unsur-Unsur Hiperbola

Irisan Kerucut Matematika Kelas 11 • Part 1: Macam-Macam (Lingkaran, Parabola, Elips, Hiperbola)

Hyperbola (Part 1) | Conic Sections | Don't Memorise

Conic sections: Intro to hyperbolas | Conic sections | Algebra II | Khan Academy

Matematika tingkat lanjut kelas XII (12) SMA /MA Kurikulum merdeka @GUcilchaNEL1964
5.0 / 5 (0 votes)