What is meant by Factorising? What is a Factor? | ExamSolutions
Summary
TLDRThis tutorial introduces the concept of factorizing algebraic expressions, explaining how it is the reverse process of expanding. The speaker walks through examples of expanding and factorizing expressions, demonstrating how to break them into factors. By comparing expanding and factorizing, the tutorial helps viewers understand how to manipulate algebraic expressions, starting with basic factorization techniques like using the highest common factor (HCF). Future tutorials will delve into more complex factorization methods.
Takeaways
- 😀 Factorizing is the opposite of expanding brackets.
- 😀 Expanding involves multiplying terms inside brackets and simplifying them into a polynomial.
- 😀 When expanding 2x(4x - 3), you get 8x^2 - 6x.
- 😀 Expanding x(x - 2) results in x^2 - 2x.
- 😀 Expanding (-3)(x - 2) gives -3x + 6.
- 😀 Factorizing 8x^2 - 6x results in 2x(4x - 3).
- 😀 Factorizing x^2 - 5x + 6 gives (x - 3)(x - 2).
- 😀 Factorizing means creating one term made up of several factors.
- 😀 In factorized form, the expression 8x^2 - 6x becomes 2x(4x - 3), with factors 2x and (4x - 3).
- 😀 Factorizing involves reversing the process of expansion to express the polynomial in terms of its factors.
- 😀 The tutorial will cover different methods of factorizing, starting with the highest common factor (HCF) approach.
Q & A
What does it mean to factorize an expression?
-Factorizing an expression means rewriting it as a product of its factors, essentially reversing the process of expansion. For example, instead of expanding the brackets, we express the result as a multiplication of simpler terms.
How would you expand the expression (2x - 3)(4x)?
-To expand the expression (2x - 3)(4x), you multiply each term inside the bracket by 4x. This gives: 2x * 4x = 8x² and -3 * 4x = -12x.
What is the expanded form of (x - 2)(x - 3)?
-To expand (x - 2)(x - 3), you multiply each term: x * x = x², x * -3 = -3x, -2 * x = -2x, and -2 * -3 = +6. After combining like terms, the expanded form is x² - 5x + 6.
What is the opposite of expanding an expression?
-The opposite of expanding an expression is factorizing it. This means you take an expanded expression and rewrite it as the product of simpler factors, essentially reversing the multiplication process.
How do you factorize 8x² - 6x?
-To factorize 8x² - 6x, first find the highest common factor (HCF) of the terms, which is 2x. Then factor out 2x, giving: 2x(4x - 3).
What are the factors of x² - 5x + 6?
-The factors of x² - 5x + 6 are (x - 3) and (x - 2). These are the two binomials that, when multiplied, will give the expanded expression.
What is meant by a term being made up of several factors?
-A term being made up of several factors means that it is expressed as the product of multiple simpler expressions. For example, the term 8x² - 6x is made up of the factors 2x and (4x - 3).
What is the highest common factor (HCF) and how does it help in factorization?
-The highest common factor (HCF) is the greatest factor that is common to all terms in an expression. It helps in factorization by allowing you to factor out the largest common term from the expression, simplifying the process.
What happens when you factorize an expression like x² - 5x + 6?
-When you factorize x² - 5x + 6, you find two binomial factors that multiply to give the original expression. In this case, the factorized form is (x - 3)(x - 2).
What will be covered in future tutorials regarding factorization?
-In future tutorials, different types of factorization will be explored, starting with the highest common factor (HCF) type. This will include how to factorize various expressions using different techniques.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Expansion - Form 2 Maths Chapter 2 Factorisation & Algebraic Fraction

Bentuk Aljabar (4) - Matematika Kelas 7

An Intro to Combining Like Terms | Simplifying Expressions by Combining Like Terms | Math with Mr. J

Expanding Brackets - Corbettmaths

SIMPLIFYING RATIONAL ALGEBRAIC EXPRESSION || GRADE 8 MATHEMATICS Q1
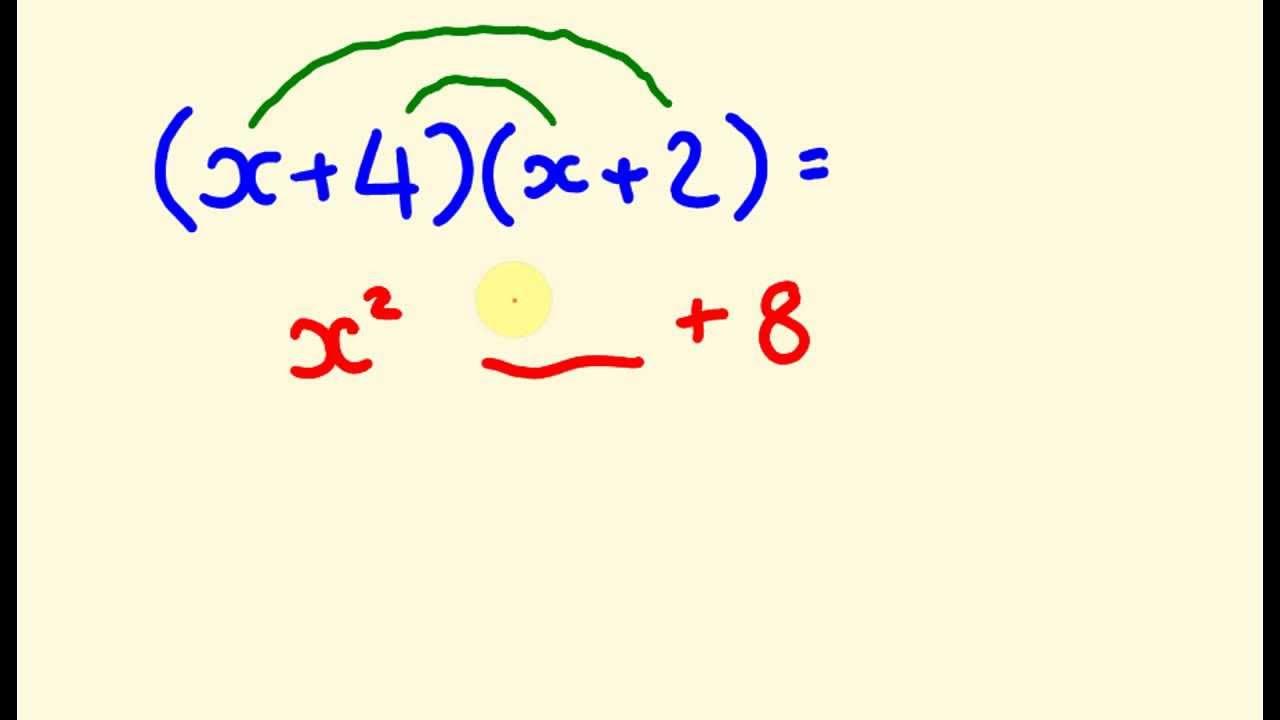
Algebra Tricks - Multiply binomials instantly!
5.0 / 5 (0 votes)