How To Solve Amazon's Hanging Cable Interview Question
Summary
TLDRIn this video, Presh Talwalkar presents a fascinating math problem about a hanging cable between two poles. He explores two cases: one where the cable is 20 meters above the ground and another where it's only 10 meters above. Using the catenary equation, Talwalkar demonstrates how to calculate the distance between the poles for the first case, resulting in 45.4 meters. For the second case, the problem leads to a logical twist, revealing that the poles are coincident when the cable is only 10 meters above the ground. The video encourages viewers to think critically before calculating.
Takeaways
- 😀 The problem discussed is about a cable of 80 meters hanging from two 50-meter poles, with the goal of calculating the distance between the poles under different conditions.
- 😀 The problem is broken down into two cases: one where the center of the cable is 20 meters above the ground, and another where it is 10 meters above the ground.
- 😀 The solution for the first case (center 20 meters above the ground) involves using symmetry, a coordinate system, and a catenary equation to calculate the distance between the poles.
- 😀 The catenary equation used in the solution is y = a * cosh(x/a) - a, with the variables representing key parameters such as the cable’s length and the distance from the poles.
- 😀 To calculate the distance between the poles, the cable is split into two equal lengths, and the problem is reduced to finding the distance from the center of the cable to one of the poles.
- 😀 A reference paper by Neil Chatterjee and Bogdan G. Nita on the hanging cable problem is mentioned as a helpful resource.
- 😀 The distance between the poles for the first case is calculated to be approximately 45.4 meters after solving for the unknown variable 'a' and using the catenary equation.
- 😀 The second case (center 10 meters above the ground) leads to an issue where the cable length is insufficient to be hung between the poles, resulting in the poles being coincident with zero distance apart.
- 😀 In this scenario, the cable folds directly downward because half of its length already exceeds the distance to the top of the pole, making the poles effectively at the same point.
- 😀 The video emphasizes the importance of logical thinking and problem-solving, noting that some employees might calculate without realizing the underlying trick in the second case.
Q & A
What is the main mathematical problem discussed in the video?
-The video discusses a problem involving a cable of 80 meters hanging between two poles that are each 50 meters tall. The goal is to calculate the distance between the two poles when the cable's center is either 20 meters or 10 meters above the ground.
What is the significance of using symmetry and a coordinate system in solving the problem?
-Symmetry simplifies the problem by allowing the cable to be split into two equal halves. Using a coordinate system centered at the cable’s center helps simplify the mathematical calculations and provides a clear way to apply the relevant formulas.
Why is the catenary equation used to model the hanging cable?
-The catenary equation models the shape of a hanging cable or chain under the influence of gravity. It describes the curve formed by the cable as it hangs between two fixed points, making it ideal for solving problems related to hanging cables.
What was the equation used to calculate the distance from the center of the cable to one of the poles?
-The equation used is: y = a * cosh(x / a) - a, where 'y' is the height, 'a' is a parameter to be solved for, and 'x' is the horizontal distance from the center of the cable to the pole.
What is the relationship between 'cosh' and 'sinh' in solving the problem?
-The hyperbolic identities 'cosh²(t) - sinh²(t) = 1' allow for the manipulation of the catenary equation and the calculation of unknown parameters. This relationship is used to derive the value of 'a' and subsequently solve for the distance between the poles.
What mathematical identity helped simplify the equations in the solution?
-The hyperbolic identity 'cosh²(t) - sinh²(t) = 1' was crucial in simplifying the equations. By substituting known values for 'cosh' and 'sinh,' the unknown parameter 'a' was determined, which helped solve for the distance 'x'.
How was the final distance between the poles calculated in case (a) where the center of the cable is 20 meters above the ground?
-After solving for the parameter 'a' and the distance 'x', the result was approximately 22.7 meters. Doubling this value gives the total distance between the two poles, which is approximately 45.4 meters.
What is the key difference between the two parts of the problem (a and b)?
-The key difference is the height of the cable’s center above the ground. In part (a), the center is 20 meters above the ground, whereas in part (b), it is 10 meters above the ground, leading to a different outcome.
Why did the problem in part (b) result in no solution?
-In part (b), when the center of the cable is 10 meters above the ground, the cable is effectively folded in half, as half of the cable’s length (40 meters) already reaches the top of the pole. This means the poles must be coincident, resulting in a distance of 0 meters between them.
What lesson does the speaker impart at the end of the video?
-The speaker emphasizes the importance of thinking logically before jumping into calculations. While many can solve the problem mechanically, it's essential to first understand the underlying concepts and think critically about the situation before applying mathematical formulas.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
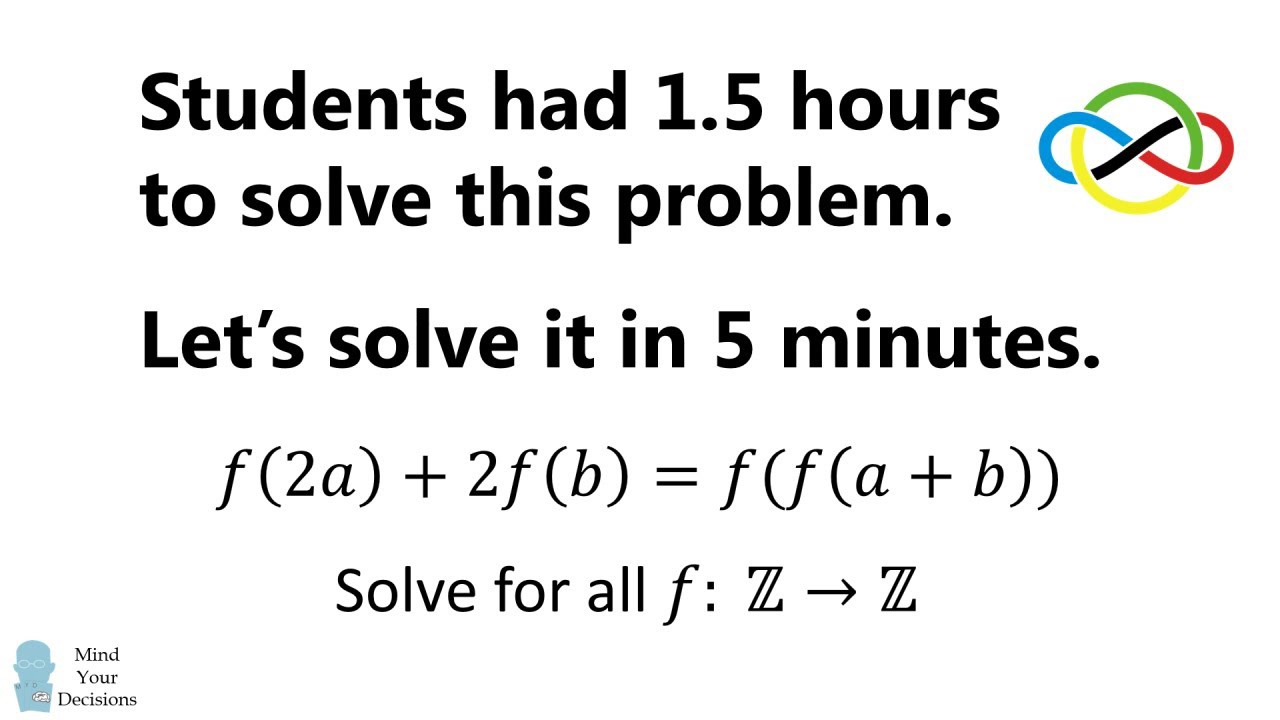
Solving An Insanely Hard Problem For High School Students

TERBARU ‼️ TES TIU (TES INTELEGENSIA UMUM) PPPK 2024 P3K - CONTOH SOAL PEMBAHASAN-KOMPETENSI TEKNIS

Remedial UH matematika

Magnetism | The Dr. Binocs Show | Educational Videos For Kids

Apa itu Magnet?

Maybe We Got Lost in Equations: The Language Barrier of Mathematics | RB Jann Jamindang | TEDxUPV
5.0 / 5 (0 votes)