[Bab I.1] RINGKASAN MATERI BILANGAN REAL DAN SOAL TKA MATEMATIKA SMA/SMK/MA/MAK 2025

Summary

This video provides a comprehensive introduction to real numbers, covering key concepts such as natural, whole, integer, rational, irrational, and real numbers. It explains the properties of real numbers—commutative, associative, and distributive—and demonstrates how these properties apply through various mathematical operations. The lesson also includes practical example questions with step-by-step explanations to enhance understanding. Designed to prepare students for the TKA mathematics exam, the video encourages viewers to engage actively and reinforces learning with a focus on cognitive levels from knowledge to reasoning.

Takeaways

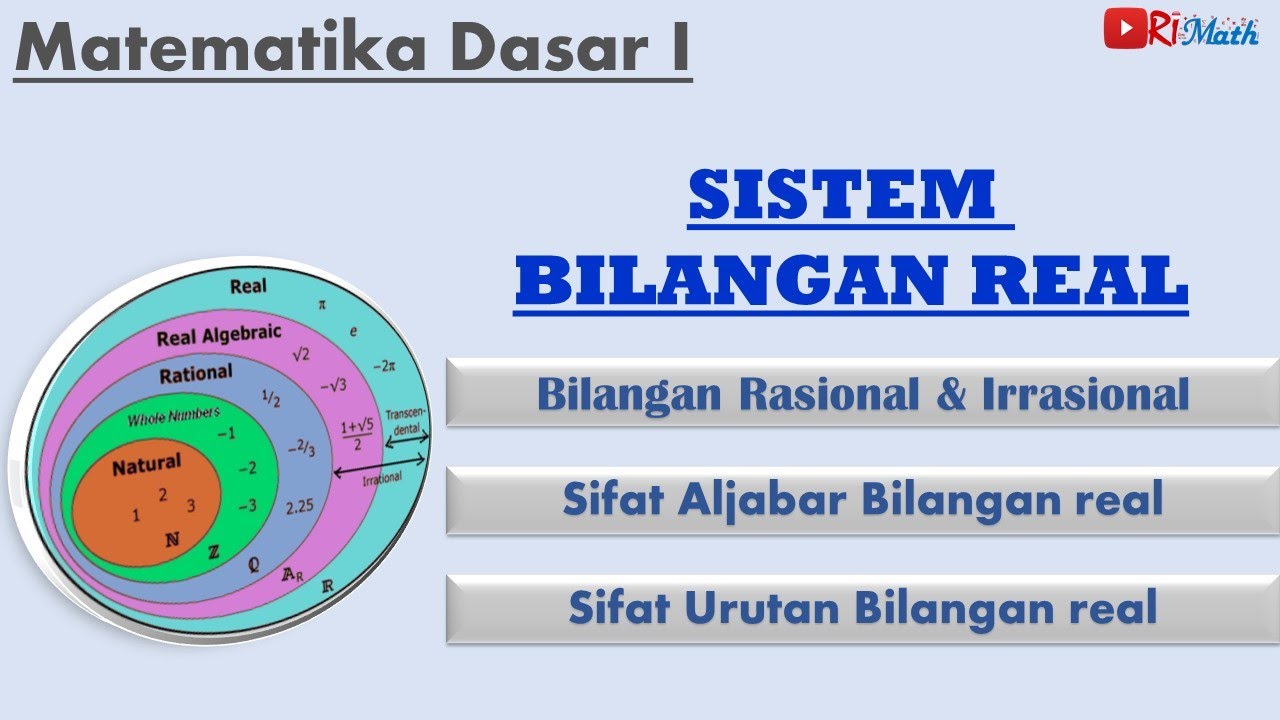
• 😀 Real numbers include all numbers that can be represented on a number line, such as natural numbers, whole numbers, integers, rational numbers, and irrational numbers.
• 😀 Natural numbers are positive numbers starting from 1 and are used for counting objects (e.g., books, pencils).
• 😀 Whole numbers are natural numbers including 0, while integers also include negative numbers.
• 😀 Rational numbers can be expressed as a fraction of two integers (a/b) and include whole numbers, ordinary fractions, and terminating decimals.
• 😀 Irrational numbers have non-repeating, non-terminating decimals, such as √2 and pi.
• 😀 The key difference between rational and irrational numbers is that irrational numbers have decimal representations that never repeat or terminate.
• 😀 Real numbers are a combination of both rational and irrational numbers.
• 😀 Mathematical operations on real numbers include addition, subtraction, multiplication, and division, and they follow certain properties like commutative, associative, and distributive properties.
• 😀 The commutative property states that the order of addition or multiplication does not affect the result, but this property does not apply to subtraction or division.
• 😀 The distributive property applies to multiplication over addition, meaning a*(b+c) equals a*b + a*c.
• 😀 Examples of practice questions were provided to help students understand concepts such as identifying rational and irrational numbers, and applying mathematical properties like distributive and associative properties.

Q & A

What is the definition of real numbers?

Real numbers include all numbers that can be expressed on a number line, encompassing natural numbers, whole numbers, integers, rational numbers, and irrational numbers.

How are natural numbers defined in the context of real numbers?

Natural numbers are the set of positive integers starting from 1 and are used primarily for counting, such as counting books, pencils, etc. They do not include zero.

What is the difference between whole numbers and integers?

Whole numbers are natural numbers plus zero, whereas integers include both positive and negative whole numbers, as well as zero.

What is a rational number?

A rational number is any number that can be expressed as a fraction 'a/b', where 'a' and 'b' are integers, and 'b' is not zero. Examples include 1/2, -3, and 0.75.

Can you explain irrational numbers with an example?

Irrational numbers cannot be expressed as a simple fraction. Their decimal expansion does not terminate or repeat. Examples include √2 and pi (π).

What is the key difference between rational and irrational numbers?

Rational numbers have decimal expansions that either terminate or repeat, while irrational numbers have decimal expansions that neither terminate nor repeat.

What are the basic operations on real numbers?

The basic operations on real numbers include addition, subtraction, multiplication, and division. These operations have specific properties, including commutative, associative, and distributive properties.

What is the commutative property in mathematics?

The commutative property states that for addition and multiplication, the order of the numbers does not change the result. For example, a + b = b + a and a * b = b * a.

What is the distributive property, and can you give an example?

The distributive property states that for multiplication over addition, a * (b + c) is the same as (a * b) + (a * c). For example, 2 * (3 + 4) = (2 * 3) + (2 * 4).

What happens when you subtract or divide numbers in terms of the commutative property?

The commutative property does not apply to subtraction or division. For example, 5 - 2 is not the same as 2 - 5, and 6 / 2 is not the same as 2 / 6.

What should we do when solving mathematical expressions with parentheses?

When solving expressions with parentheses, you should always perform the operations inside the parentheses first, following the order of operations (PEMDAS/BODMAS).

What does the associative property refer to in mathematics?

The associative property refers to how the grouping of numbers in an operation does not affect the result. For example, in addition, (a + b) + c = a + (b + c), and similarly for multiplication.

Why is it important to remember that division and subtraction do not follow the commutative property?

It’s crucial to remember because switching the order of operations in division and subtraction changes the result. For example, 3 - 2 ≠ 2 - 3 and 6 / 2 ≠ 2 / 6.

What is the significance of understanding rational and irrational numbers in mathematics?

Understanding rational and irrational numbers is crucial because it helps distinguish between numbers that can be precisely written as fractions and those whose decimal representations are infinite and non-repeating, like √2 and pi.

How would you identify a distributive property expression from a list?

To identify a distributive property expression, look for multiplication that applies to addition or subtraction, like a * (b + c). For example, 3 * (4 + 5) follows the distributive property.