Materi:Himpunan Penyelesaian Sistem Pertidaksamaan Linear (Dua) Variabel" (SPTLDV) Kelompok-1

Summary

In this presentation, Arya Eki from group 1 of class 10 TKJ explains the concept of solving linear inequalities in two variables. The discussion focuses on understanding the terms 'inequality,' 'linear,' and 'two variables.' Arya illustrates the process of solving an inequality like 3X + 2Y ≥ 6 using graphical methods, such as finding the intercepts and using a Cartesian plane. The group also tests possible solutions and identifies the feasible region for the inequality. The session concludes with a polite acknowledgment of potential errors and an invitation for feedback.

Takeaways

• 😀 The speaker begins by greeting the audience in multiple languages and introducing themselves as part of a group from class 10 TKJ.
• 😀 The topic of the presentation is the solution set for systems of linear inequalities involving two variables.
• 😀 The speaker explains why the term 'inequality' is used, referring to symbols like '>', '>=', '<', '<=' and '≠'.
• 😀 The explanation includes why the term 'linear' is used, stating that the highest power of the variables (x, y) is 1.
• 😀 A linear equation will form a straight line when plotted, while higher powers like x² or y² will result in curves.
• 😀 The speaker introduces the concept of 'two variables' and mentions that equations with three variables (e.g., x + y + z) are not considered linear in this context.
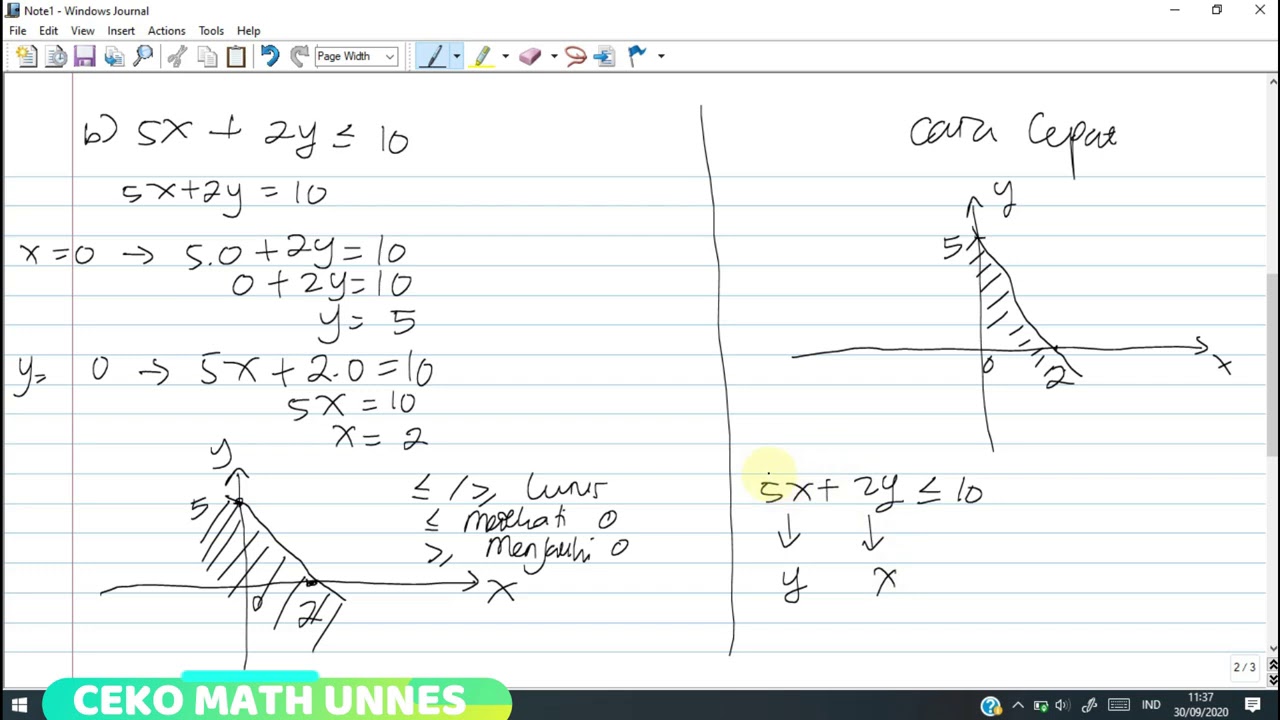
• 😀 A worked example is provided to demonstrate how to find the x and y intercepts for the inequality 3x + 2y ≥ 6.
• 😀 To find the y-intercept, the speaker substitutes x = 0 and solves for y, getting y = 3.
• 😀 Similarly, to find the x-intercept, y is set to 0, and after solving for x, the result is x = 2.
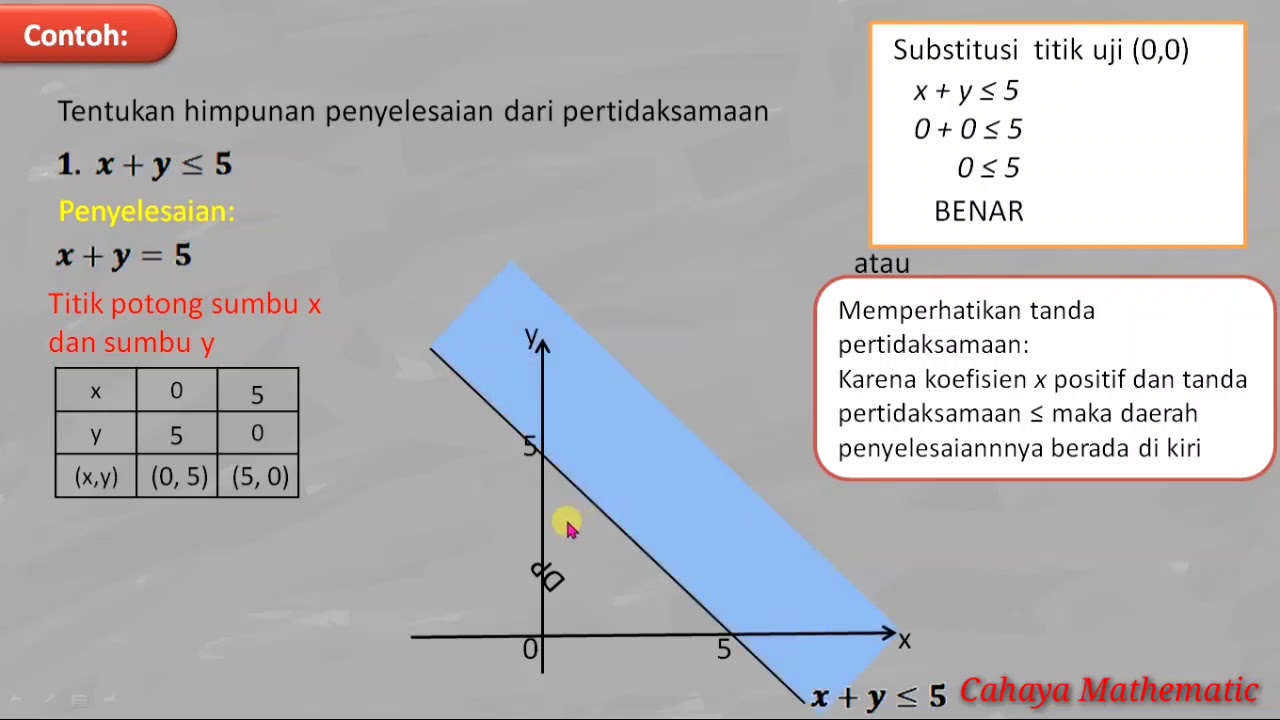
• 😀 The speaker discusses the process of graphing these points on the Cartesian plane and mentions that the inequality should be checked with a test point like (0, 0).
• 😀 After testing the inequality with the point (0, 0), the speaker concludes that the region of the solution set lies on one side of the line, explaining how to interpret the result visually.

Q & A

What is the main topic discussed in the video script?

The main topic of the video script is the solution set of linear inequality systems in two variables, specifically focusing on the concept of 'himpunan penyelesaian' (solution set).

Why is the system referred to as 'pertidaksamaan' (inequality)?

It is called 'pertidaksamaan' because it uses inequality symbols such as 'greater than', 'greater than or equal to', 'less than', 'less than or equal to', and 'not equal to'.

What does 'linier' (linear) refer to in this context?

'Linier' refers to the system being linear because the highest power of the variables (X and Y) is 1. If the highest power were 2 (like X² or Y²), the system would be non-linear.

Why is the system considered to have two variables?

The system is considered to have two variables because it includes two variables (X and Y), as opposed to a system with three or more variables.

How is the solution set for the linear inequality 3X + 2Y ≥ 0 determined?

The solution set is determined by finding the points where the equation intersects the x-axis and y-axis, and then identifying the region that satisfies the inequality.

How do you find the x-intercept for the inequality 3X + 2Y ≥ 0?

To find the x-intercept, set Y = 0 and solve for X. For the equation 3X + 2Y = 6, this results in X = 2, so the x-intercept is (2,0).

How do you find the y-intercept for the inequality 3X + 2Y ≥ 0?

To find the y-intercept, set X = 0 and solve for Y. For the equation 3X + 2Y = 6, this results in Y = 3, so the y-intercept is (0,3).

What does the point (0, 3) represent in the context of the graph?

The point (0, 3) represents the y-intercept, meaning the value of Y when X is 0 in the equation 3X + 2Y = 6.

What does the point (2, 0) represent in the context of the graph?

The point (2, 0) represents the x-intercept, meaning the value of X when Y is 0 in the equation 3X + 2Y = 6.

Why is the inequality symbol changed during the solution process?

The inequality symbol is changed to an equality sign (≥) during the process to simplify the solving of the equation, helping to identify the points of intersection before returning to the inequality for the final solution.