AP Precalculus – 4.2 Parametric Functions Modeling Planar Motion
Summary
TLDRIn this educational video, the instructor explains how to solve a quadratic equation, focusing on finding both the x-intercepts and y-intercepts. The equation is factored into two binomials, allowing the identification of the intercepts. The process includes verifying results through substitution and graphical representation, with a detailed walkthrough of each calculation. The instructor uses a visual approach, adjusting the graph's window to clearly show the intercepts and provide further validation. This lesson offers a step-by-step guide to understanding quadratic functions and their properties.
Takeaways
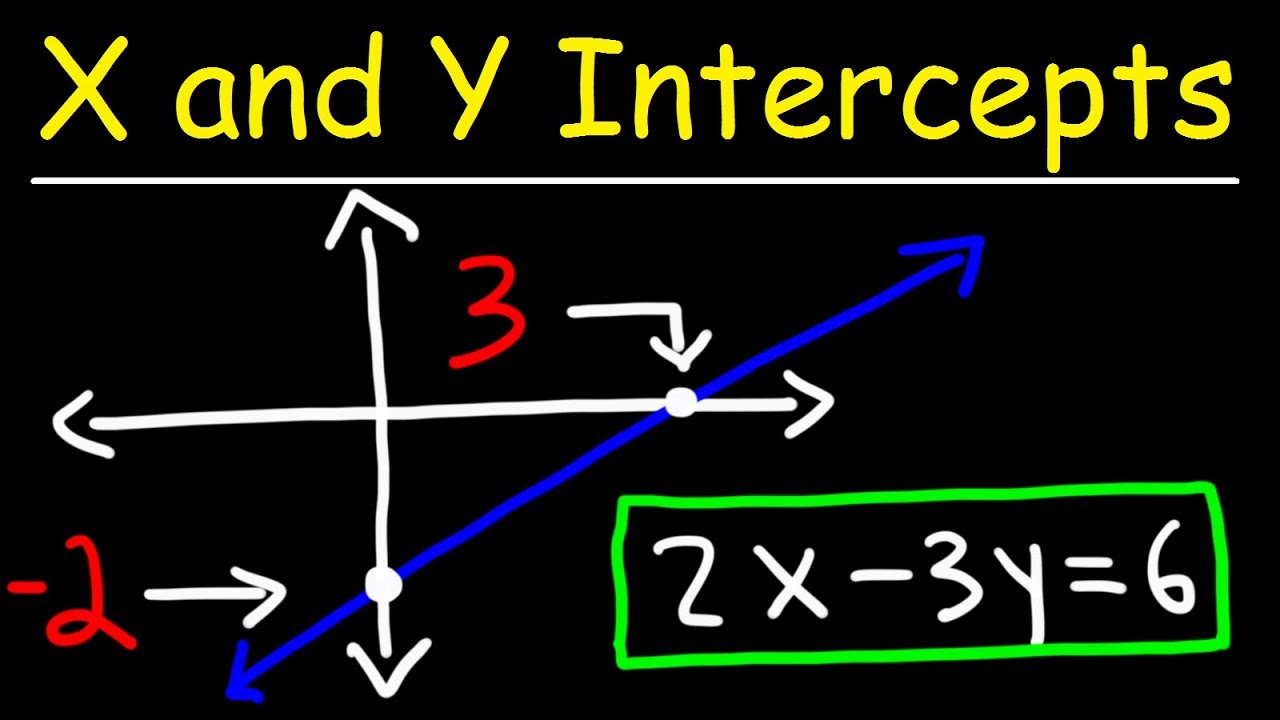
- 😀 The quadratic equation can be factored into two binomials: (t + 3)(t + 2) = 0.
- 😀 Solving the factored equation gives two t-values: t = -3 and t = -2.
- 😀 For a y-intercept, the first coordinate is always 0, so we plug in the values of t to find the corresponding y-values.
- 😀 The first y-intercept is (0, 1) when t = -3.
- 😀 The second y-intercept is (0, 2) when t = -2.
- 😀 The x-intercept is (2, 0), which is found by solving the factored quadratic equation.
- 😀 Graphing the quadratic equation helps to visually verify the x and y intercepts.
- 😀 The graph is zoomed in with X and Y values ranging from -3 to 3 for better clarity.
- 😀 The video highlights the process of solving quadratic equations using factoring, which is a straightforward method.
- 😀 After verifying the intercepts on the graph, it confirms that the solutions for the intercepts are correct.
- 😀 The instructor concludes the lesson by encouraging students to keep practicing and mastering the concept of quadratic equations.
Q & A
What method is used to solve the quadratic equation in this script?
-The method used is factoring the quadratic equation. The equation factors to (t + 3)(t + 2) = 0.
What are the two solutions for the quadratic equation?
-The two solutions for the quadratic equation are t = -3 and t = -2.
How do you find the y-intercepts from the factored equation?
-The y-intercepts are found by substituting the values of t into the equation y = t + 4 when t = -3 and t = -2. This gives the points (0, 1) and (0, 2).
Why is the first coordinate of the y-intercept always zero?
-The first coordinate of the y-intercept is always zero because the y-intercept occurs where the value of x (or t in this case) is 0.
What are the x-intercepts for this equation?
-The x-intercepts are t = -3 and t = -2, as these are the values of t that make the equation (t + 3)(t + 2) = 0 true.
How does the graph verify the intercepts?
-The graph verifies the intercepts by showing the points where the curve crosses the x-axis (x-intercepts) and the y-axis (y-intercepts). In this case, the x-intercepts are at t = -3 and t = -2, and the y-intercepts are at y = 1 and y = 2.
What changes were made to the graph's window to improve visibility?
-The graph's window was adjusted by changing the X-Men and Y-Men values from their default to a range of -3 to 3, allowing a better view of the intercepts.
What is the purpose of adjusting the graph's window settings?
-The purpose of adjusting the graph's window settings is to zoom in and get a clearer view of the intercepts, making it easier to confirm the results.
What role does factoring play in solving this problem?
-Factoring plays a key role in solving this problem because it allows the equation to be simplified into two smaller equations, making it easier to solve for the intercepts.
What mathematical concept does this script illustrate, and what is its practical application?
-This script illustrates the concept of solving quadratic equations to find intercepts, which is a fundamental skill in algebra used to understand the behavior of functions and graphing.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)