Métodos de Runge-Kutta
Summary
TLDREn esta clase se explican los métodos de ruta para la solución numérica de ecuaciones diferenciales ordinarias. Se destaca la importancia de reducir el error de aproximación, detallando métodos como el de Boyle modificado y el punto medio. Se presentan diferentes técnicas de aproximación, incluyendo el método de cuarto orden, el cual utiliza evaluaciones ponderadas de derivadas para mejorar la precisión. También se menciona cómo estos métodos son fundamentales en la resolución de problemas de valor inicial, con ejemplos prácticos y un enfoque en la computación eficiente utilizando herramientas como MATLAB.
Takeaways
- 😀 Los métodos de Runge-Kutta son una familia de métodos para la solución numérica de ecuaciones diferenciales ordinarias que requieren más cálculos para aproximar la solución en cada punto de red.
- 😀 El objetivo principal de los métodos de Runge-Kutta es reducir el error local de aproximación utilizando sumas ponderadas de funciones derivadas.
- 😀 Los métodos de Euler modificado y el punto medio forman parte de la familia de métodos Runge-Kutta de segundo orden, donde el error de aproximación se controla a través de la ponderación de derivadas.
- 😀 El método de Euler modificado utiliza un promedio de las derivadas para aproximar la derivada de la función en el nodo, mientras que el punto medio calcula la derivada en el punto medio del intervalo.
- 😀 En los métodos de segundo orden de Runge-Kutta, el valor de la derivada se aproximó utilizando la función evaluada en puntos intermedios del intervalo.
- 😀 El método de Runge-Kutta de orden 4 requiere realizar cuatro evaluaciones de la función en diferentes puntos a lo largo del intervalo para obtener una aproximación más precisa.
- 😀 Los métodos de Runge-Kutta de orden superior, como el de cuarto orden, permiten mejorar significativamente la precisión de la aproximación, con errores que disminuyen con el incremento de h.
- 😀 El orden de un método Runge-Kutta se refiere al número de términos utilizados en la suma ponderada, y un mayor orden implica menor error en la aproximación.
- 😀 El método de Runge-Kutta de cuarto orden (RK4) es particularmente efectivo, aunque más costoso computacionalmente, porque involucra varias evaluaciones de la función en distintos puntos del intervalo.
- 😀 La ecuación de diferencia del método de Runge-Kutta de cuarto orden incluye una combinación ponderada de las derivadas evaluadas en puntos iniciales y medios del intervalo, lo que mejora la aproximación.
- 😀 En la práctica, los métodos de Runge-Kutta se utilizan ampliamente debido a su efectividad, y el método de cuarto orden es el más comúnmente aplicado para resolver ecuaciones diferenciales en sistemas complejos.
Q & A
¿Qué son los métodos de ruta y cuál es su objetivo principal?
-Los métodos de ruta son una familia de métodos numéricos utilizados para aproximar soluciones de ecuaciones diferenciales. Su objetivo principal es reducir el error local de aproximación, lo que justifica el mayor esfuerzo computacional requerido para calcular la solución en cada punto de la red.
¿Cuáles son los métodos que forman parte de la familia de métodos de ruta?
-Los métodos de Boyle modificados y el método del punto medio forman parte de la familia de métodos de ruta.
¿Cómo se interpreta la función de incremento en los métodos de ruta?
-La función de incremento se puede interpretar como una pendiente representativa en el intervalo de cálculo. Esta función depende del valor de h, y su comportamiento se ajusta a medida que se cambia el valor de h, lo que afecta directamente a la aproximación de la solución.
¿Cuál es la diferencia entre el método de Euler modificado y el método del punto medio?
-El método de Euler modificado utiliza un promedio de las derivadas para aproximar la derivada de la función, mientras que el método del punto medio calcula la derivada en el punto medio del intervalo, mejorando la aproximación al considerar un punto intermedio.
¿Qué significa que un método sea de 'orden 2' en el contexto de los métodos de ruta?
-Que un método sea de orden 2 significa que utiliza dos términos en la ponderación para aproximar la solución. En estos métodos, el error de aproximación disminuye proporcionalmente con el cuadrado de h, lo que mejora la precisión al disminuir el tamaño del paso.
¿Cómo se relacionan los métodos de ruta de orden 2 con los polinomios de Taylor?
-Los métodos de ruta de orden 2 se derivan utilizando el polinomio de Taylor de segundo orden, lo que permite obtener fórmulas de aproximación que consideran el comportamiento de la función en un intervalo y ayudan a minimizar el error de aproximación.
¿Por qué los métodos de Euler modificado y el punto medio son efectivos en la práctica?
-Estos métodos son efectivos porque han demostrado ser útiles para resolver ecuaciones diferenciales con precisión razonable, equilibrando el costo computacional y la reducción del error de aproximación. Son ampliamente utilizados debido a su fiabilidad en la práctica.
¿Qué es el método de cuarto orden y cómo mejora la aproximación?
-El método de cuarto orden utiliza una combinación ponderada de derivadas evaluadas en varios puntos dentro del intervalo de cálculo. Este método mejora la aproximación al reducir el error de manera más eficiente, con una disminución del error proporcional a h elevado a la cuarta potencia, lo que lo hace más preciso con pasos más pequeños.
¿Cómo se calcula la aproximación de la solución utilizando el método de cuarto orden?
-Para calcular la aproximación en el método de cuarto orden, se evalúa la función en cuatro puntos diferentes dentro del intervalo, luego se ponderan estos valores utilizando coeficientes específicos (1/6) para obtener la nueva aproximación. Este proceso requiere cuatro evaluaciones de la función para cada nodo.
¿Cuáles son los desafíos de usar el método de cuarto orden en la práctica?
-Uno de los desafíos del método de cuarto orden es que requiere más cálculos por cada nodo, ya que es necesario realizar cuatro evaluaciones de la función, lo que aumenta el costo computacional en comparación con métodos de menor orden. Sin embargo, este mayor esfuerzo se justifica por la precisión mejorada que ofrece.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Método de Runge-Kutta de 4to orden para solución de EDO's

ECUACIONES DIFERENCIALES EXACTAS. Curso completo de ecuaciones diferenciales desde cero

0. ¿Qué es una Ecuación Diferencial? Tipos de ecuaciones diferenciales, solución de ED

Ecuaciones diferenciales | Introducción
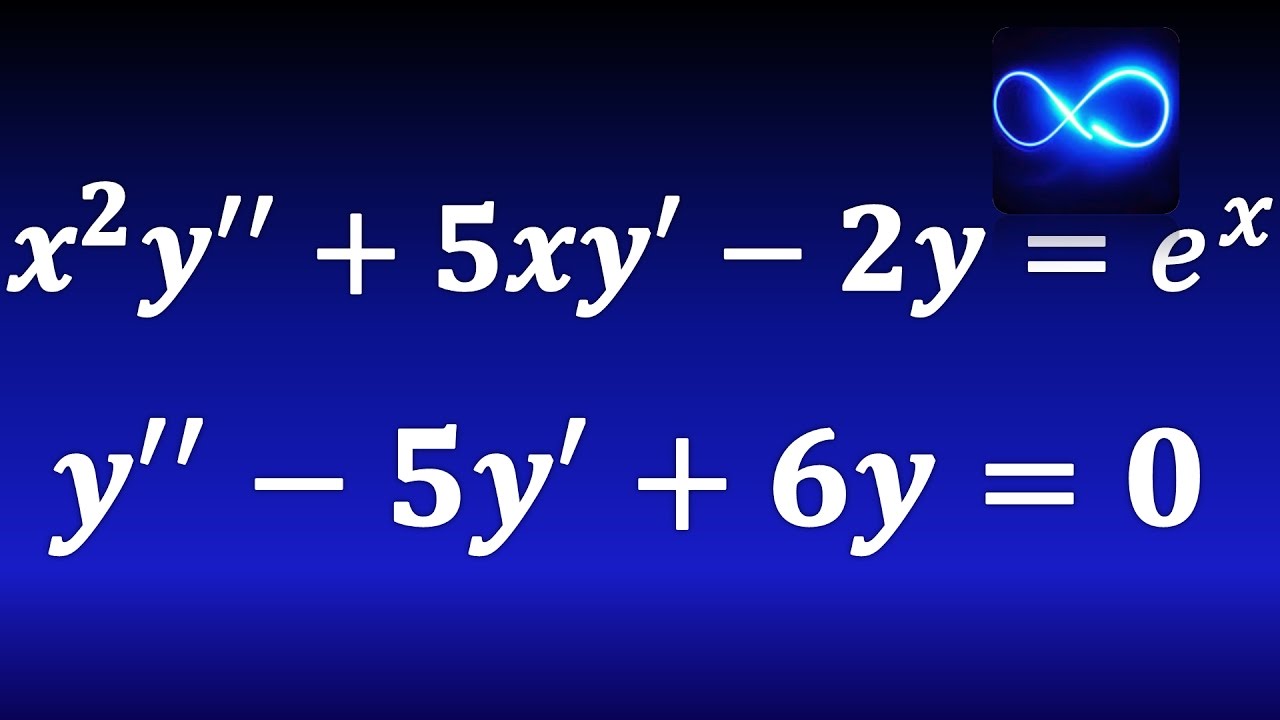
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes

Ecuaciones diferenciales simples
5.0 / 5 (0 votes)
