BISSETRIZ INTERNA DE UM TRIÂNGULO \Prof.Gis/

Summary

In this educational video, the instructor explains the internal angle bisector theorem of a triangle, breaking down the proportional relationships between the triangle's sides and segments created by the bisector. The lesson includes step-by-step guidance on solving related exercises, from basic proportion setups to more complex quadratic equations. Viewers are encouraged to master foundational concepts like bisectors and proportions for a thorough understanding of the theorem. The instructor emphasizes the importance of understanding prior mathematical knowledge and offers tips for successful study and problem-solving strategies in geometry.

Takeaways

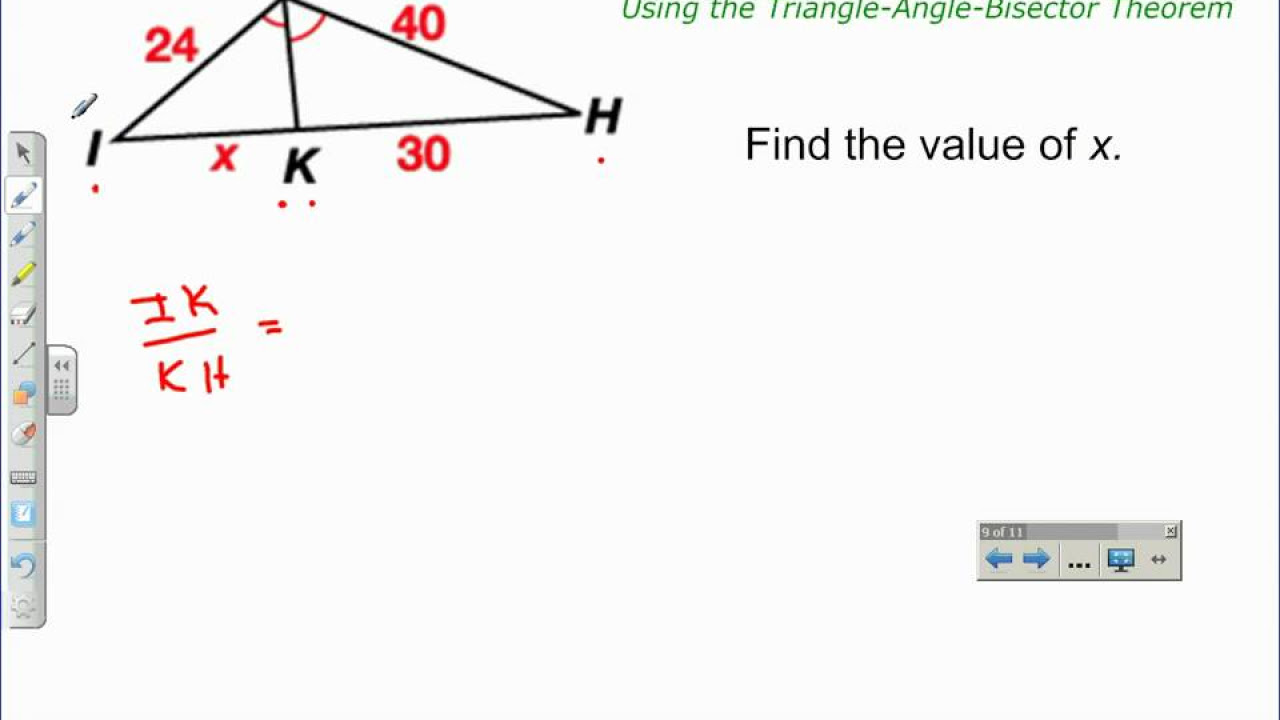
• 😀 The internal bisector theorem divides an internal angle of a triangle into two equal parts.
• 😀 The theorem states that the bisector of an angle in a triangle creates proportional segments on the opposite side.
• 😀 Proportions formed by the segments on the opposite side are based on the sides of the triangle that form the considered angle.
• 😀 A common way to form a proportion in this theorem is by comparing the sides of the triangle to the segments on the opposite side.
• 😀 When solving problems using this theorem, the proportions can be written as: AB/BS = AS/SC, or AB/BC = BS/SC.
• 😀 In practical problems, you can solve by multiplying the proportional terms crosswise to find unknown values.
• 😀 Example 1: Given that AB = 4, BS = 2, and AS = 10, you can calculate SC using the proportion, finding SC = 5.
• 😀 Example 2: In another problem, BC = 4, CP = 3.2, and BA = x, you calculate x by setting up a proportion and solving the equation.
• 😀 Some exercises involve more complex equations, like second-degree equations, where the solution requires knowledge of algebraic manipulation.
• 😀 It is crucial to understand and apply proportionality and basic algebraic concepts when using the bisector theorem to solve triangle-related problems.

Q & A

What is the internal bisector theorem in a triangle?

The internal bisector theorem states that an angle bisector of a triangle divides the opposite side into segments that are proportional to the adjacent sides of the triangle.

Why is it important to understand previous mathematical concepts before learning the internal bisector theorem?

It is important because the internal bisector theorem builds upon earlier concepts, such as understanding bisectors and proportions. Without a strong foundation in these areas, the theorem will be harder to comprehend.

How does an angle bisector divide a triangle?

An angle bisector divides the angle into two equal parts and creates proportional segments on the opposite side of the triangle.

How are the segments formed by the bisector related to the sides of the triangle?

The segments formed on the opposite side by the bisector are proportional to the adjacent sides of the triangle. For example, in triangle ABC, the angle bisector creates segments on side BC that are proportional to the sides AB and AC.

How do you form a proportion using the internal bisector theorem?

To form a proportion, you compare the ratio of the sides of the triangle with the segments created by the bisector. For instance, if AB is the side of the triangle, and BF and FC are the segments created by the bisector, you can form a proportion like AB/BF = AC/FC.

Can different proportions be used in the internal bisector theorem?

Yes, there are different ways to form proportions, and the results will be the same. You could use either AB/BF = AC/FC or AB/BC = BF/FC, depending on your preference.

What is the importance of proportions in solving problems with the bisector theorem?

Proportions allow you to relate the sides and segments of a triangle to find unknown values. Solving these proportions helps in calculating missing lengths and understanding the triangle's geometry.

How can you solve a problem using the internal bisector theorem?

First, write the proportion according to the bisector theorem. Then, apply cross-multiplication to solve for the unknown value, using algebraic methods such as simplifying fractions or solving equations.

What is the method to solve for 'x' when given a proportional equation?

You can solve for 'x' by cross-multiplying the two sides of the proportion. For example, if you have 4/x = 2/5, you multiply 4 by 5 and 2 by x, then solve the resulting equation to find 'x'.

How do you handle equations with decimals in the bisector theorem?

When dealing with decimals, it is helpful to multiply both the numerator and denominator by 10 (or another appropriate power of 10) to eliminate the decimal. This makes the equation easier to solve.