PT3 KSSM Mathematics Form 1 (Algebraic Expressions) Chapter 5 Complete Revision

Summary

In this educational video, Teacher Daisy introduces Form 1 Mathematics, focusing on Chapter 5: Algebraic Expressions. The video covers essential concepts like variables, algebraic expressions, terms, coefficients, like and unlike terms, and how to simplify and solve algebraic expressions. Students learn to represent variables, identify fixed and varied values, and perform basic arithmetic operations such as addition, subtraction, multiplication, and division in algebraic expressions. The content is designed to help learners understand algebraic fundamentals with practical examples and problems. Viewers are encouraged to engage with the material and ask questions in the comments.

Takeaways

• 😀 Algebraic expressions are mathematical phrases combining numbers, variables, and operations, but they do not include equality or inequality signs.
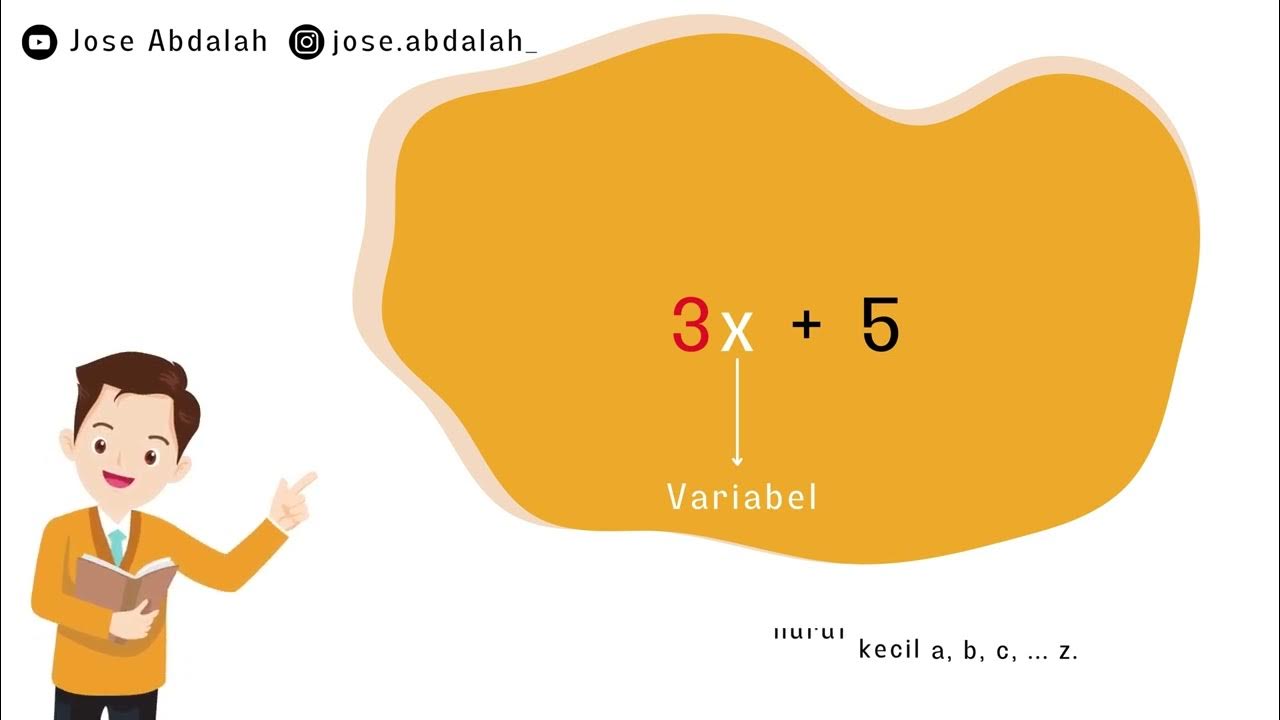
• 😀 A variable is a symbol used to represent a value that can change. For example, in the context of algebraic expressions, 'n' can represent the number of sweets in a jar.
• 😀 An algebraic expression can be represented by symbols like letters, where each symbol stands for a number or a changing quantity.
• 😀 To determine whether a variable has a fixed or varied value, you must analyze the context. For example, the annual interest rate is fixed, but the traveling time can vary.
• 😀 Algebraic expressions can be created for real-life situations. For example, the total cost of apples and oranges can be expressed algebraically as 5x + 8y.
• 😀 The value of an algebraic expression can be calculated by substituting known values for the variables, as shown in the example of finding the value of 8x - 5y + 7.
• 😀 Terms in an expression are individual parts that are either numbers or variables. Coefficients are the numbers multiplied by variables.
• 😀 Like terms are terms that have the same variable and exponent. For example, 7x, x, and -4x are like terms because they all involve the variable x.
• 😀 Unlike terms have different variables or exponents. For example, 2x and 2x^2 are unlike terms because their exponents differ.
• 😀 To simplify algebraic expressions, first group like terms, then perform the necessary operations such as addition or subtraction.
• 😀 Multiplication and division of algebraic expressions involve gathering like variables and performing operations on the coefficients. This can lead to expressions like 12a^4b^3.

Q & A

What is an algebraic expression?

An algebraic expression is a mathematical phrase that combines numbers and/or variables using mathematical operations, such as addition, subtraction, multiplication, and division. It does not contain equality or inequality signs.

What is a variable in an algebraic expression?

A variable is a letter or symbol used to represent a value that can change. It is often used in algebraic expressions to denote unknown or changing quantities.

Can you give an example of an algebraic expression involving variables and numbers?

An example of an algebraic expression is 5x + 8y, where x and y are variables representing quantities, and 5 and 8 are coefficients multiplying the respective variables.

How do you identify fixed and varied values for a variable?

A fixed value is constant and does not change, such as the annual interest rate for a fixed deposit. A varied value changes, like the travel time to school, which differs each day.

How do you simplify an algebraic expression?

To simplify an algebraic expression, combine like terms—terms that have the same variables raised to the same power—and then perform the arithmetic operations (addition or subtraction) on these terms.

What is the meaning of terms and coefficients in an algebraic expression?

A term is either a number or a variable in an algebraic expression. A coefficient is the numerical factor multiplying a variable. For example, in 5x, 5 is the coefficient, and x is the variable.

What are like terms and unlike terms?

Like terms are terms that have the same variables and exponents, such as 3x and -4x. Unlike terms have different variables or exponents, like 2x and 2y.

What is the result of simplifying the expression 3x + 5y + 8x - y - 9?

Simplifying the expression involves combining like terms: 3x + 8x = 11x and 5y - y = 4y. The result is 11x + 4y - 9.

How do you perform multiplication of algebraic expressions?

To multiply algebraic expressions, multiply the coefficients (numbers) and then multiply the variables. For example, in 3ab^2 * 4a^3b, multiply the numbers (3 * 4 = 12) and then combine the variables (a^1 * a^3 = a^4, b^2 * b^1 = b^3), resulting in 12a^4b^3.

What is the quotient of algebraic expressions, and how do you simplify it?

The quotient of algebraic expressions is found by dividing the terms. To simplify, cancel out common factors from the numerator and denominator. For example, in 20m^4n^2 / 5m^2n^3, divide the coefficients (20 / 5 = 4) and subtract the exponents of common variables (m^4 / m^2 = m^2, n^2 / n^3 = 1/n), resulting in 4m^2/n.