L18 - Dyanamics - Lesson 18 - Rigid Body Kinematics

Summary

In Lesson 18 of ES 310, the focus shifts to the study of rigid bodies and their kinematics, particularly rotational motion. The lesson covers key concepts such as angular velocity, angular acceleration, and the relationship between linear and angular quantities. The instructor explains how rigid bodies undergo both translation and rotation, providing mathematical relations for velocities and accelerations. Examples, such as a gear system and a window mechanism, demonstrate how these principles apply to real-world problems. The lesson also includes a discussion of the motion of rigid bodies using various methods like kinematic equations and angular velocity calculations.

Takeaways

• 😀 Rigid bodies are collections of particles that maintain their shape and orientation during motion, unlike particles which can be considered as points with no internal structure.
• 😀 The motion of rigid bodies involves both translation and rotation, and in many cases, both motions are combined into general planar motion.
• 😀 In translation, every point in the rigid body moves in the same direction, with velocity and acceleration being the same for all points in the body.
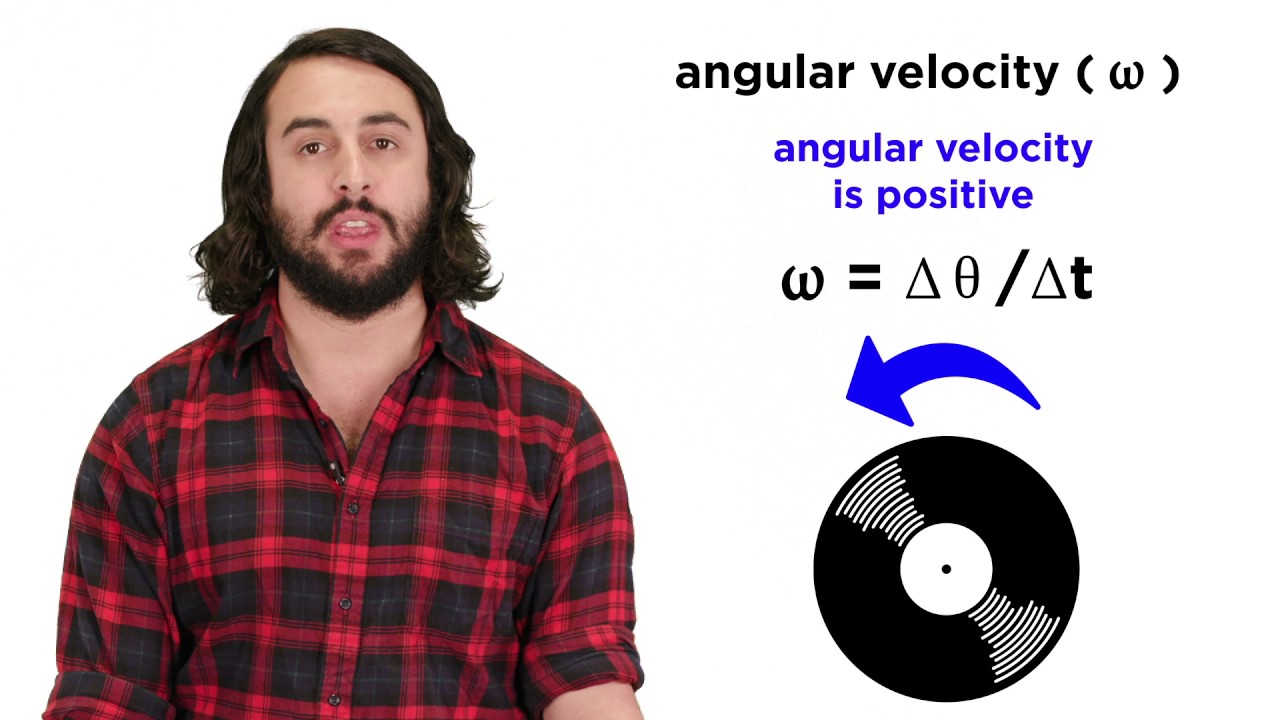
• 😀 Rotation involves defining angular displacement (θ) relative to a reference line, and the angular velocity (ω) and angular acceleration (α) are derived as time derivatives of θ and ω, respectively.
• 😀 The relationship between linear motion and rotational motion is key in kinematics: the linear speed (v) of a point on a rotating body is related to the angular velocity by the equation v = ω * r, where r is the radius of rotation.
• 😀 Tangential acceleration (at) is the product of angular acceleration (α) and radius (r), while normal acceleration (an) is proportional to the square of angular velocity and the radius of rotation.
• 😀 The total acceleration of a point in a rotating body combines both tangential and normal components, and can be calculated using vector notation with cross products.
• 😀 Kinematic equations for rigid bodies can be used to calculate motion in both translation and rotation, with the same approach applied to rotational variables as with linear motion.
• 😀 When working with gear systems, angular velocities and accelerations are linked through meshing gears. The motion of one gear impacts the motion of connected gears.
• 😀 Practical examples, such as rolling up a car window with a hand crank, show the application of rotational motion principles to everyday mechanical systems.
• 😀 In more complex gear systems, angular accelerations can be propagated through connected shafts, and the kinematic equations help calculate the time, angular velocity, and number of revolutions for the entire system.

Q & A

What is the main focus of Lesson 18 in this course?

The main focus of Lesson 18 is on rigid bodies and their kinematics, specifically looking at rotational motion, rotational speed, and acceleration, and how these relate to linear speeds and accelerations.

What is the distinction between particles and rigid bodies in motion?

Particles are treated as point masses with no shape or orientation, while rigid bodies are collections of particles that retain their shape and orientation as they move, including rotational motion.

What are the two types of motion that rigid bodies exhibit?

Rigid bodies exhibit two types of motion: translation (where the entire body moves along a straight or curved path) and rotation (where the body rotates about an axis).

How is rotational speed defined in the context of rigid bodies?

Rotational speed is defined as the angular velocity, which is the time derivative of the angular position (theta). It is typically represented by the symbol Omega (Ω).

What are the key relationships between linear and angular motion?

The relationship between linear and angular motion is as follows: linear velocity (V) is related to angular velocity (Ω) by the equation V = RΩ, where R is the radius. Similarly, linear acceleration (a) is related to angular acceleration (α) by the equation a = Rα.

How do you calculate the tangential and normal components of acceleration for rotating rigid bodies?

Tangential acceleration is calculated as a_t = Rα, where α is angular acceleration and R is the radius. Normal acceleration is calculated as a_n = RΩ², where Ω is the angular velocity and R is the radius.

What is the importance of the cross product in the context of rotational motion?

The cross product is important when calculating velocity and acceleration in rotational motion because it accounts for the direction of motion. For example, the velocity vector is given by the cross product of the angular velocity vector and the radius vector.

In the example involving a car window crank, how is the angular velocity of the spur gear calculated?

The angular velocity of the spur gear is calculated by dividing the linear velocity of the cog's outer surface (V = 0.01 m/s) by the radius of the spur gear (R = 0.5 m), resulting in an angular velocity of 0.02 rad/s.

How do you determine the velocity of the window in the car window crank example?

The velocity of the window is determined by taking the Y-component of the tangential velocity of point A on the rod, which is constrained to move only in the Y-direction. Using the given angular velocity and the radius, the Y-component of the velocity is found to be 0.34 m/s.

How does the system of meshed gears in the example help determine the angular velocities of different gears?

The angular velocities of meshed gears are related through their radii. By knowing the angular acceleration of one gear, you can calculate the angular acceleration of the connected gear using the formula α_B = (R_A / R_B) * α_A, where R_A and R_B are the radii of the gears and α_A is the angular acceleration of gear A.