Metode linear programing | Metode Simplex | Matematika Bisnis | OR 2022

Summary

This video explains the Simplex Method for solving linear programming problems. The lecturer covers the process of transforming objective functions and constraints into an appropriate mathematical form, adding slack variables, and constructing a Simplex table. The video demonstrates iterating through the Simplex method to find the optimal solution for a linear programming problem, using a detailed example involving a company's revenue function and constraints. The explanation focuses on selecting the pivot column and row, updating values, and checking for optimality. By the end, the optimal solution is found, ensuring the highest possible value for the objective function.

Takeaways

• 😀 Linear programming is a method widely used in managerial decision-making and research, aimed at solving optimization problems.
• 😀 The Simplex method is specifically used when there are many variables and constraints, helping to find the optimal solution.
• 😀 The first step in applying the Simplex method is to convert the objective function and constraints into equations and add slack variables.
• 😀 Slack variables are used to convert inequality constraints into equalities, making the problem solvable via the Simplex method.
• 😀 The Simplex tableau is used to organize and solve the linear programming problem, with columns for variables and rows for constraints and the objective function.
• 😀 The key steps in the Simplex method include selecting the pivot column (key column) and pivot row (key row) to iterate towards the optimal solution.
• 😀 The key column is selected based on the smallest negative value in the objective function row, while the key row is chosen by calculating the ratio of the right-hand side to the pivot column coefficients.
• 😀 Iterating the Simplex method involves updating the tableau by changing values based on the pivot element, moving towards an optimal solution.
• 😀 A table is considered optimal when no negative values remain in the objective function row, signaling that further iterations are not needed.
• 😀 The Simplex method continues iterating until all coefficients in the objective function row are non-negative, confirming the optimal solution. The final result includes values for decision variables and the maximum or minimum value of the objective function.

Q & A

What is Linear Programming (LP)?

Linear Programming is a mathematical method used to determine the best outcome in a model with linear relationships, typically used for optimization problems such as maximizing profits or minimizing costs under given constraints.

What is the Simplex method in Linear Programming?

The Simplex method is an iterative algorithm used to solve optimization problems in Linear Programming. It is used when there are many variables and constraints, and it helps find the optimal solution by moving from one vertex of the feasible region to another.

When should you use the Simplex method over the graphical method?

The Simplex method is preferred when there are more than two variables or complex constraints, where the graphical method would not be feasible or practical.

What does the objective function represent in Linear Programming?

The objective function represents the goal of the optimization, such as maximizing profit or minimizing cost. In the script, it is given as a linear equation in terms of decision variables (e.g., Z = 8X1 + 6X2).

How are inequalities converted in Linear Programming problems?

Inequalities in Linear Programming are converted into equalities by introducing slack variables. These variables represent the unused portion of the resources in constraints and are added to the system of equations.

What are slack variables?

Slack variables are introduced to convert inequality constraints into equalities in Linear Programming problems. They represent the difference between the left-hand side and the right-hand side of a constraint when the constraint is not fully utilized.

What is the first step in the Simplex method?

The first step in the Simplex method is to rewrite the objective function and all constraints as equations by adding slack variables, ensuring all functions are in the standard form for the Simplex tableau.

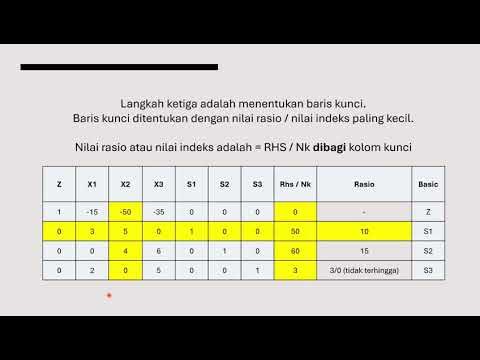
How is the key column selected in a Simplex tableau?

The key column is selected by identifying the variable in the objective function row that has the most negative coefficient. This indicates the variable that should enter the solution to increase the objective function most effectively.

How is the key row selected in a Simplex tableau?

The key row is selected by dividing the value in the right-hand column (the 'value of constraints') by the value in the key column for each row. The row with the smallest positive quotient is chosen as the key row.

What does it mean for a Simplex tableau to be optimal?

A Simplex tableau is considered optimal when there are no more negative coefficients in the objective function row, meaning no further improvement can be made to the solution.

How do you update the Simplex tableau during iterations?

During each iteration, the key column and key row are used to update the tableau. The values in the key row are divided by the key element (the number where the key row and key column intersect), and the other rows are adjusted by subtracting appropriate multiples of the key row to maintain the system of equations.

What is the significance of the value of the objective function at the optimal solution?

At the optimal solution, the value of the objective function represents the maximum or minimum value of the quantity being optimized (e.g., maximum profit, minimum cost), and the values of the decision variables correspond to the optimal allocation of resources.