UJAR KALKULUS 2 PERTEMUAN 9 INTEGRAL PARSIAL TAK TENTU

Summary

In this episode of 'Ujar Umpan Mengajar,' Eko Haris Sutopo introduces the concept of indefinite partial integrals, focusing on key steps for solving such integrals. The lesson covers the method of integration by parts, explaining the process of choosing the correct substitutions for u and v. Through several examples, viewers are shown how to solve integrals like ∫x cos(x) dx and ∫x² sin(x) dx. Emphasizing the importance of proper substitution, the video concludes by reinforcing the need for practice to fully grasp the concept of partial integration in Calculus 2.

Takeaways

• 😀 Introduction to the concept of integration by parts (integral parsial tak tentu).
• 😀 Integral by parts is used when substitution integration fails or is difficult.
• 😀 The formula for integration by parts is integral u dv = uv - integral v du.
• 😀 The correct selection of functions for u and v is crucial in simplifying the integration process.
• 😀 First example: integral of x cos x dx. The solution involves making appropriate substitutions for u and dv.
• 😀 The importance of choosing the right u and dv to avoid creating more complex integrals.
• 😀 Second example: integral of x^2 e^(2x) dx. The solution utilizes integration by parts step-by-step.
• 😀 Third example: integral of x^2 sin x dx. Demonstrates multiple steps of integration by parts.
• 😀 Each integration by parts requires careful substitution to avoid complications in the process.
• 😀 The takeaway is that practice in selecting u and v simplifies the solving of integration by parts problems.
• 😀 Summary: Proper substitution and technique are essential for mastering integration by parts in Calculus 2.

Q & A

What is the main topic of the video script?

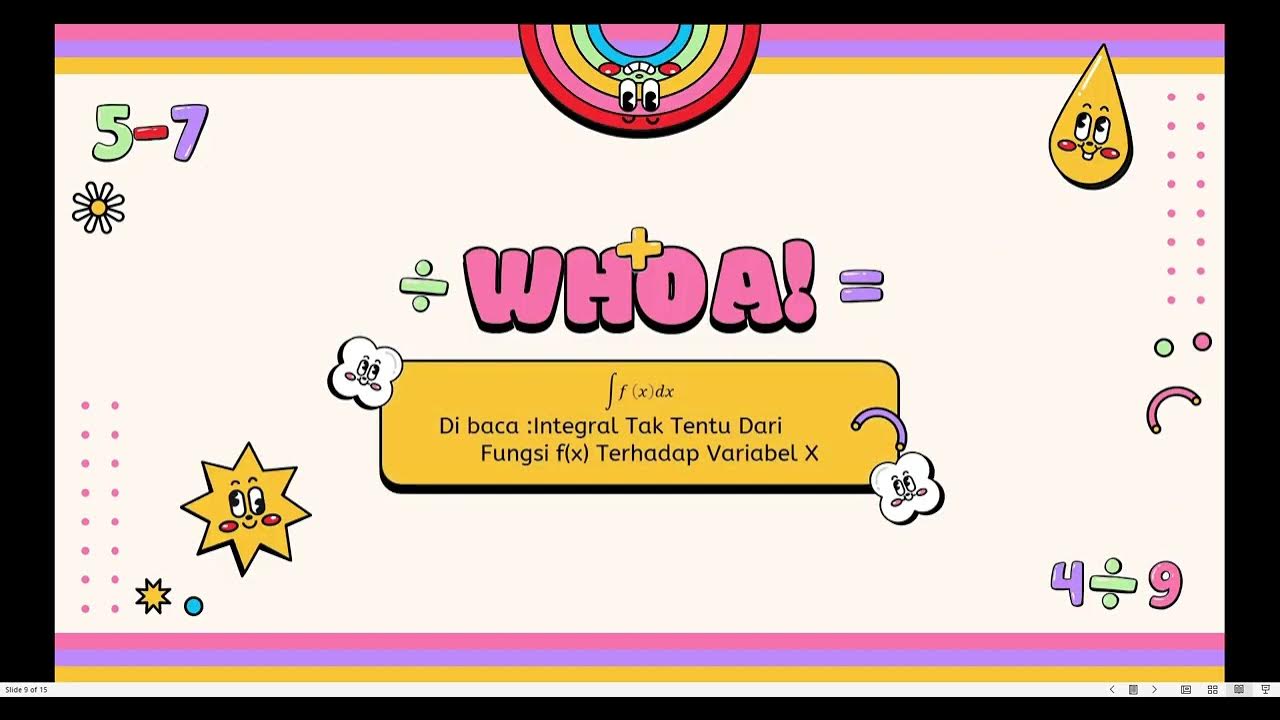
The main topic of the video script is about learning and understanding the concept of 'Indefinite Partial Integral' as part of the Calculus 2 curriculum.

What is the purpose of the video program?

The purpose of the video program is to help students understand and solve problems related to indefinite partial integrals, with step-by-step explanations and examples.

What are the two key points discussed in the session?

The two key points discussed in the session are: 1) The definition of indefinite partial integrals, and 2) The steps involved in solving indefinite partial integral problems.

What is integral partial substitution, and when is it used?

Integral partial substitution, also known as double substitution, is used when standard integration by substitution fails or becomes difficult. It helps to break down more complex integrals into simpler forms for easier resolution.

What is the importance of selecting 'u' and 'v' in partial integral problems?

The selection of appropriate 'u' and 'v' is crucial as it simplifies the integration process. A poor choice can lead to more complicated integrals, making the solution more difficult to obtain.

Can you explain the general formula for solving an indefinite partial integral?

The general formula for solving an indefinite partial integral is: ∫udv = uv - ∫vdu, where 'u' and 'v' are functions chosen from the integrand, and 'du' and 'dv' represent their respective derivatives.

What was the first example problem presented in the video?

The first example problem presented was to find the integral of x * cos(x) dx. The solution involved making substitutions u = x and dv = cos(x) dx, and applying the formula to simplify the integral.

How did the video resolve the integral of x^2 * e^(2x) dx?

In the solution to the integral of x^2 * e^(2x) dx, the substitution u = x and dv = e^(2x) dx was used, leading to the result: 1/2 * x * e^(2x) - 1/4 * e^(2x) + C.

What is the significance of choosing the correct 'u' and 'v' in the examples?

Choosing the correct 'u' and 'v' is essential to prevent complications in the integral. The video emphasizes that an improper choice can make the integral more complex, as seen in the failed attempt with cos(x) as 'u'.

What is the takeaway message from the video regarding solving indefinite partial integrals?

The takeaway message is that to solve indefinite partial integrals efficiently, it is crucial to make the right substitutions for 'u' and 'v' to simplify the integral. This approach minimizes the chances of encountering more complicated integrals.