Trabalho de uma força constante

Summary

This video lesson explains the concept of work done by a constant force in physics, breaking it down into four distinct cases. It covers the formula for calculating work, which involves force, displacement, and the cosine of the angle between them. The script provides examples with varying angles, including 0°, 60°, 180°, and 90°, to demonstrate how these factors affect the work done. The lesson emphasizes understanding how direction and angle influence the magnitude of work, providing practical examples and highlighting key points for students to grasp the concept of work in physics.

Takeaways

• 😀 Work is calculated using the formula W = F * d * cos(θ), where F is force, d is displacement, and θ is the angle between the force and displacement vectors.
• 😀 When the force and displacement are in the same direction (θ = 0°), the work done is simply W = F * d.
• 😀 If the force is applied at an angle, the cosine of the angle must be included in the calculation (W = F * d * cos(θ)).
• 😀 For an angle of 60° between force and displacement, cos(60°) = 0.5, reducing the work done to half of what it would be in the same direction.
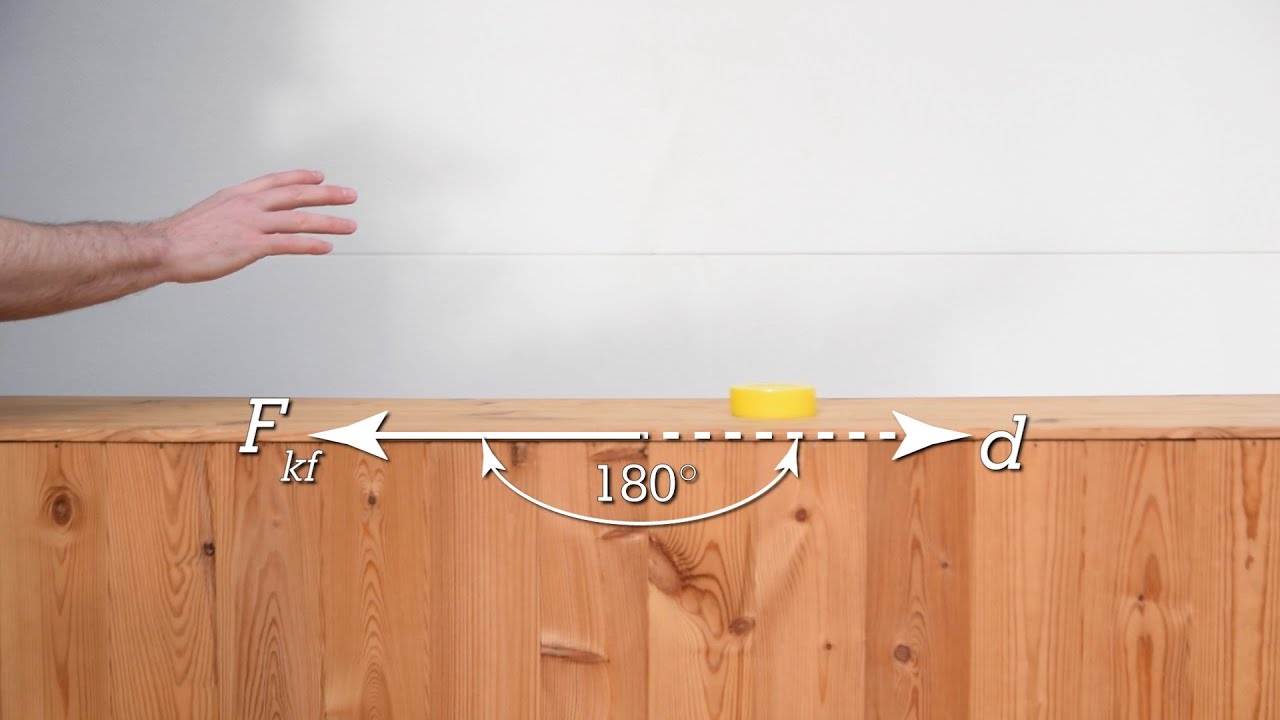
• 😀 When the force opposes the displacement (θ = 180°), cos(180°) = -1, resulting in negative work.
• 😀 Negative work indicates that the force is acting opposite to the direction of displacement, essentially 'slowing down' the object.
• 😀 If the force and displacement are perpendicular to each other (θ = 90°), the work done is zero because cos(90°) = 0.
• 😀 It’s important to understand and memorize common cosine values for angles such as 0°, 30°, 45°, 60°, 90°, and 180° for easier calculations.
• 😀 The unit of work is Joules (J), where 1 Joule equals 1 Newton meter (1 J = 1 N·m).
• 😀 Understanding the direction and angle of the applied force relative to displacement is crucial in determining the work done in physics problems.

Q & A

What is the formula for calculating work done by a constant force?

The formula for calculating work (W) done by a constant force is W = F × d × cos(θ), where F is the force applied, d is the displacement, and θ is the angle between the force vector and the displacement vector.

How does the angle between the force and displacement vectors affect the work done?

The angle θ plays a crucial role in the work calculation. If the angle is 0° (force and displacement are in the same direction), the work is maximized. If the angle is 90° (force is perpendicular to displacement), the work done is zero. If the angle is 180° (force and displacement are in opposite directions), the work is negative.

What does it mean when the work is negative?

Negative work occurs when the force applied to an object is in the opposite direction of its displacement. This typically happens when the force is resisting the motion, like friction.

In the first example, what is the work done by a force of 8 N over a displacement of 3 meters with no angle between them?

In this case, since the angle is 0° (force and displacement are in the same direction), the work is W = F × d = 8 N × 3 m = 24 J (Joules).

In the second example, the force has an angle of 60° with the horizontal. How is the work calculated in this case?

When the angle is 60°, the work is calculated as W = F × d × cos(60°). The force is 8 N, the displacement is 3 meters, and cos(60°) equals 0.5. So, the work is W = 8 × 3 × 0.5 = 12 J.

Why is the work calculated in the second example smaller than in the first one?

The work is smaller because the angle between the force and the displacement reduces the effective component of the force in the direction of displacement. A 60° angle results in only half of the force contributing to the work.

What happens when the angle between the force and displacement is 180°?

When the angle is 180°, the force and displacement are in opposite directions, meaning the work done is negative. For example, if the force is 8 N and the displacement is 3 meters, the work would be W = - 8 × 3 = -24 J.

In the third example, why is the work negative when the angle is 180°?

The work is negative because the force is applied in the opposite direction to the displacement. In this case, the force resists the displacement, making the work negative.

What happens when the angle between the force and displacement is 90°?

When the angle is 90°, the force is perpendicular to the displacement, and no work is done. This is because cos(90°) equals 0, so the work is W = F × d × cos(90°) = 0, regardless of the magnitude of the force or displacement.

In the fourth example, why is the work done zero when the force is vertical and the displacement is horizontal?

The work is zero because the force is perpendicular to the displacement. Since the angle is 90°, cos(90°) equals 0, meaning that no work is done, even though there is a force applied.