USAHA DAN ENERGI - FISIKA - MATERI UTBK SBMPTN DAN SIMAK UI

Summary

This video explains the concept of work and energy in physics, focusing on how work is defined and calculated. It introduces the relationship between force, displacement, and work, with the formula W = F * S. Examples include calculating work done by forces that may or may not be aligned with the direction of displacement, such as in cases of pulling a block or pushing against a wall. The video also discusses various forces acting on objects, including normal force, friction, and gravity, using practical scenarios and detailed problem-solving methods.

Takeaways

• 😀 Work (Usaha) in physics is defined as the force applied on an object causing it to move, calculated as the product of force and displacement: W = F * S.
• 😀 The unit of work is the Joule (J), where 1 Joule equals 1 Newton-meter (N·m).
• 😀 Work is only done if there is a displacement of the object in the direction of the applied force. If there is no displacement, like in the case of pushing a wall, the work is zero.
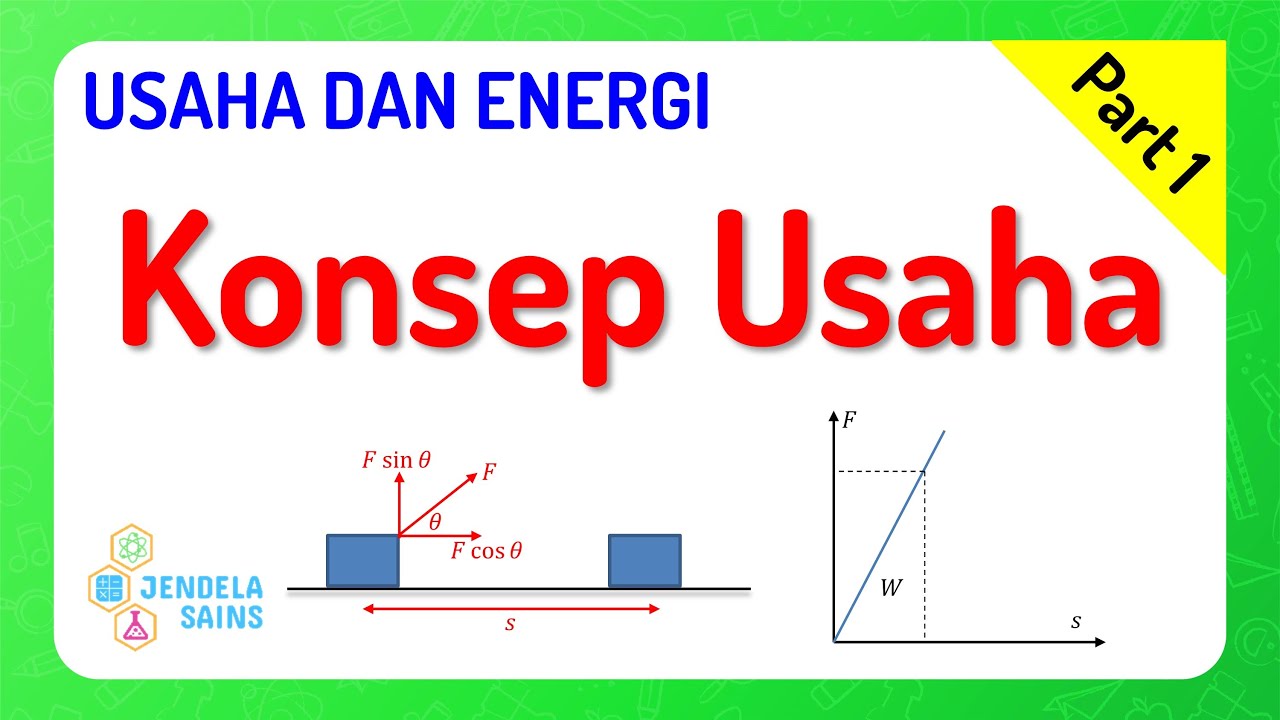
• 😀 When the applied force is at an angle to the direction of displacement, only the component of the force in the direction of displacement contributes to the work, calculated as W = F * S * cos(θ).
• 😀 The cosine of the angle between the applied force and displacement vector determines how much of the force contributes to the work. If the force is perpendicular to displacement, no work is done.
• 😀 A practical example shows a block being pulled on a frictionless surface, and how to calculate the work done when the applied force is at an angle of 60° to the horizontal.
• 😀 The work done by a force can be broken down into components along the horizontal (cosine component) and vertical (sine component) axes when there is an angle.
• 😀 When a block is pulled on a rough surface, the normal force, gravitational force, friction, and applied force all contribute to the overall work, which must be calculated step by step.
• 😀 The normal force, if perpendicular to the direction of displacement, does no work (cos(90°) = 0), as shown in the example with a waiter holding a tray.
• 😀 The total work on an object can be found by summing the work done by all forces acting on it, such as the applied force, friction, and gravity, taking their directions into account.

Q & A

What is the definition of work (usaha) in physics as explained in the video?

Work (usaha) in physics is defined as the force applied to an object that causes the object to move, specifically resulting in displacement. It is the product of force (F) and displacement (s), expressed by the formula W = F * s, where W is work measured in joules, F is the force in newtons, and s is the displacement in meters.

Why does pushing a stationary wall result in zero work?

Pushing a stationary wall results in zero work because while force is applied, the wall does not move. Since work is the product of force and displacement, and the displacement is zero in this case, the total work done is also zero.

What happens when the direction of force is not aligned with the direction of displacement?

When the direction of force is not aligned with the direction of displacement, the work done is calculated by taking the component of the force that is parallel to the displacement. This is done by projecting the force onto the direction of displacement, which is given by the formula W = F * cos(θ) * s, where θ is the angle between the force and the displacement.

How is the work done by a force on a block with an inclined angle calculated?

When a block is pulled by a force at an angle, the work done is calculated by projecting the force onto the direction of displacement. The force is broken down into its horizontal and vertical components, and the work is calculated using the formula W = F * cos(θ) * s, where θ is the angle between the force and the horizontal direction, and s is the displacement.

In the example with a 2 kg block being pulled on a smooth surface, what is the formula used to calculate the work done by the applied force?

The work done by the applied force on the 2 kg block is calculated using the formula W = F * cos(θ) * s. In the example, the force is 40 N, the angle θ is 60°, and the displacement is 5 meters, so the work done is W = 40 * cos(60°) * 5 = 100 joules.

What role does the angle between the applied force and the horizontal direction play in calculating work?

The angle between the applied force and the horizontal direction affects the effective component of the force that contributes to work. The horizontal component is given by F * cos(θ), which means that only the part of the force that is aligned with the displacement direction does work.

What are the factors involved in calculating the work done when the surface is rough?

When the surface is rough, the work done also includes the force of friction, which opposes the motion. The work done by friction is negative because it acts in the opposite direction of displacement. The force of friction is calculated using the formula f_friction = μ * N, where μ is the coefficient of friction and N is the normal force.

In the case of the 4 kg block being pulled on a rough surface, how is the normal force (N) calculated?

The normal force is calculated by considering the vertical forces acting on the block. The total vertical force must sum to zero for equilibrium. Using the equation N + F * sin(θ) - mg = 0, where N is the normal force, F is the applied force, θ is the angle of application, and mg is the weight of the block, the normal force is found to be 16 N.

Why is the work done by the normal force always zero?

The work done by the normal force is always zero because the normal force is perpendicular to the direction of displacement. Since work is calculated as the product of force and displacement, and the angle between the normal force and displacement is 90°, the cosine of 90° is zero, making the work done by the normal force zero.

How do you calculate the total work done on the block considering all the forces involved?

The total work done on the block is the sum of the work done by all forces acting on the block. This includes the work done by the applied force (F), the frictional force, the normal force (which is zero), and the weight of the block (which is also zero in the direction of displacement). The total work in this case is the sum of the individual works, yielding a total of 144 joules.