Understanding B-Trees: The Data Structure Behind Modern Databases
Summary
TLDRThis video explores the structure and function of B-trees, a data structure used to efficiently store and search large amounts of data. It compares binary search trees with B-trees, explaining how B-trees can store multiple keys per node and reduce search space more effectively. The video discusses how B-trees maintain balance through recursive node splitting and merging, ensuring efficient performance even as data grows. The principles behind B-tree insertions, deletions, and tree balancing highlight their advantages in databases and file systems, offering a deeper understanding of their operation.
Takeaways
- 😀 Binary search trees (BST) are a popular data structure that helps organize data efficiently for fast searching.
- 😀 A binary search tree follows the rule that keys to the left of a node are smaller, and keys to the right are larger.
- 😀 In a binary search tree, search operations are efficient as the search space is halved at each step.
- 😀 B-trees improve on binary search trees by allowing each node to store multiple keys, which makes the tree shallower and more efficient.
- 😀 The key advantage of B-trees is their ability to quickly cut down the search space, leading to fewer node comparisons during searches.
- 😀 B-trees maintain balance by ensuring all leaf nodes are at the same level, preventing deeper branches on one side.
- 😀 Nodes in B-trees can hold up to a maximum number of keys, and the minimum number of keys is half of that maximum.
- 😀 Inserting a key into a B-tree may cause a node to split if it exceeds its maximum number of keys, and the middle key is pushed up into the parent.
- 😀 Deleting keys from a B-tree requires ensuring nodes don’t fall below the minimum key count. If necessary, nodes can merge or borrow keys from siblings.
- 😀 B-trees are highly efficient for storing and navigating large datasets, especially in databases and file systems, where fast data retrieval is critical.
Q & A
What is the primary advantage of a binary search tree?
-The primary advantage of a binary search tree (BST) is that it allows for efficient searching by dividing the data into two parts at each step, focusing only on the relevant half of the search space.
Why might a ternary tree (a tree with three branches instead of two) not always be more efficient than a binary search tree?
-While a ternary tree might seem more efficient because it reduces the search space to a third, it requires more comparisons at each node, as each node would need to compare against two keys instead of one. This can result in more comparisons overall, reducing efficiency in certain contexts.
How does the B-tree improve upon the binary search tree in terms of data retrieval?
-A B-tree improves data retrieval by allowing nodes to store multiple keys, reducing the number of nodes to be accessed and thus speeding up the search process. The tree is also shallower than a binary search tree, leading to fewer node accesses during search operations.
What is the role of the 'minimum' and 'maximum' number of keys in a B-tree node?
-Each node in a B-tree must contain a number of keys that falls between a minimum and maximum value. The minimum ensures that nodes aren't too sparse, while the maximum ensures that the tree remains balanced and efficient. The minimum is typically half of the maximum number of keys, rounded down.
What happens when a node in a B-tree exceeds its maximum number of keys?
-When a node exceeds its maximum number of keys, it is split into two nodes. The middle key of the split node is pushed up into the parent node, which may also require splitting if it exceeds its capacity.
How does the B-tree handle splitting when the parent node is also full?
-When the parent node is full, the splitting process is recursive. The parent is split into two nodes, and the middle key is pushed up into a new root node. This ensures that the B-tree remains balanced, with all leaves at the same level.
What ensures that the B-tree remains balanced during insertions and deletions?
-The B-tree remains balanced because its leaves are always at the same level. Insertions typically happen at the bottom level, and when nodes become full, they split. Deletions involve either borrowing keys from siblings or merging nodes to maintain balance.
What happens when a key is deleted from a node that has the minimum number of keys in a B-tree?
-When a key is deleted from a node with the minimum number of keys, the node will have fewer than the required minimum. To fix this, the B-tree either borrows a key from a sibling node or merges the node with a sibling if borrowing is not possible.
How does the B-tree handle deletion when the key is not in a leaf node?
-When deleting a key from a non-leaf node, the key must be replaced with a new separator, which is either the largest key from the left subtree or the smallest key from the right subtree. Afterward, the deletion process might require borrowing from siblings or merging nodes to maintain the minimum key requirement.
Why is the B-tree particularly useful for large datasets, such as those found in databases and file systems?
-The B-tree is well-suited for large datasets because it minimizes the number of node accesses required for searching, inserting, or deleting keys. By allowing nodes to hold multiple keys, it keeps the tree shallow, improving performance and reducing the number of expensive data retrieval operations.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
I/O Structure in Operating system || Computer System Organization || Operating System

L-3.7: Introduction to Trees (Binary Tree, Almost Complete Binary Tree, Full BT, Complete BT, BST)

Lec-127: Introduction to Hadoop🐘| What is Hadoop🐘| Hadoop Framework🖥

Consistent Hashing | The Backend Engineering Show
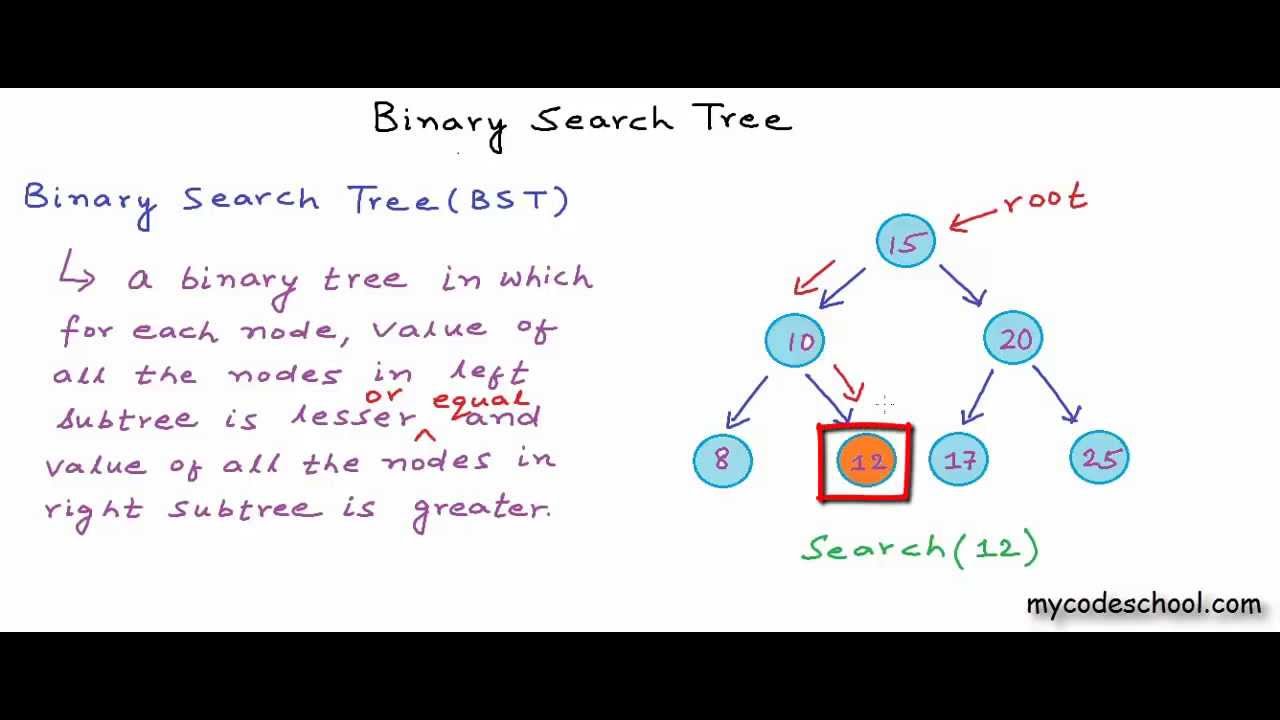
Data structures: Binary Search Tree

Merkle Tree Explained Simply | Code Eater - Blockchain | Hindi
5.0 / 5 (0 votes)