Juring Lingkaran - Matematika SMA Kelas XI Kurikulum Merdeka
Summary
TLDRIn this educational video, the concept of a sector (juring) of a circle is explained. The instructor details how a sector is formed by two radii and an arc, and how to calculate its area using the formula: Area = (α/360) × πr², where α is the central angle and r is the radius. The video also walks through a practical example, demonstrating how to compute the area of a sector with a given radius and central angle. This explanation helps students grasp both the theoretical and practical aspects of calculating a sector's area.
Takeaways
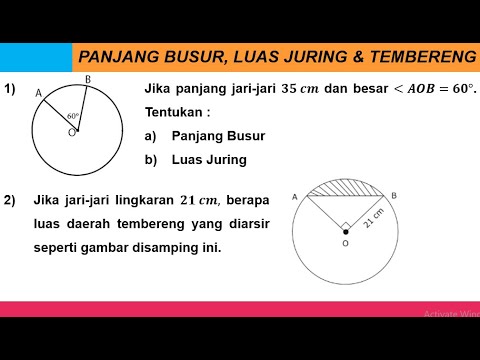
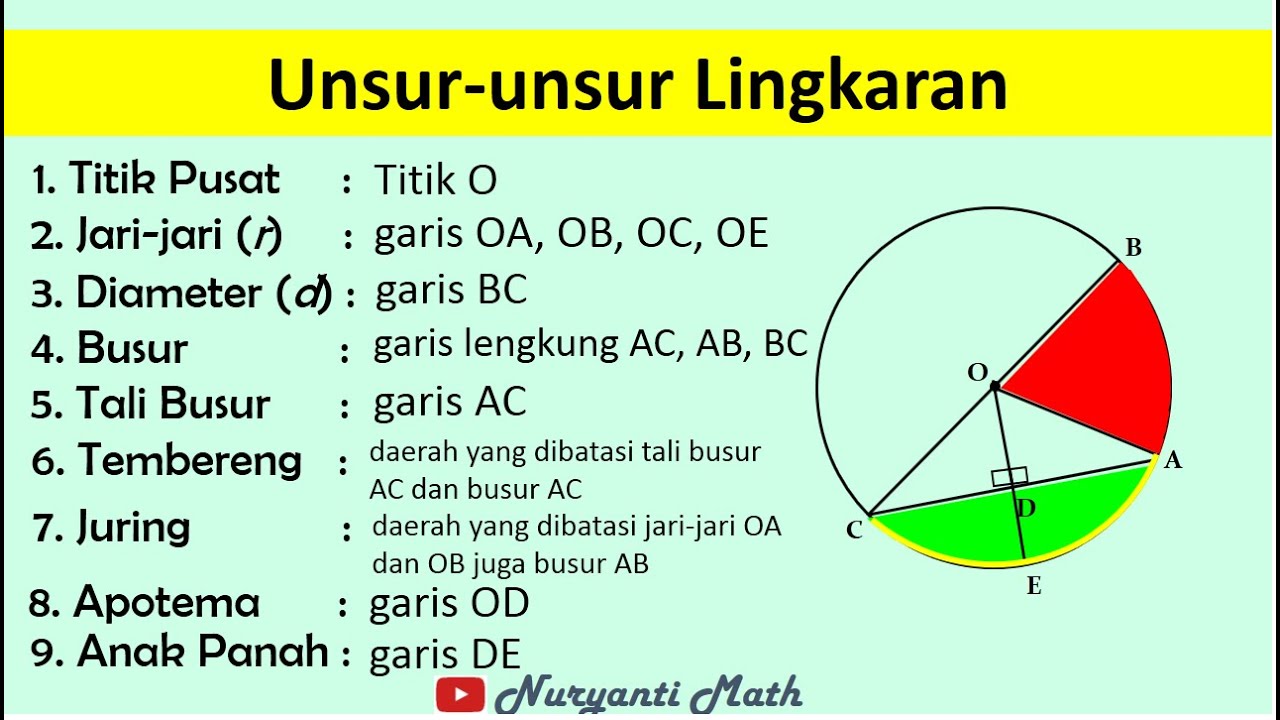
- 😀 A *juring* (sector) is the area within a circle bounded by two radii and one arc.
- 😀 The central angle of a sector is formed at the circle’s center between the two radii.
- 😀 To find the area of a sector, use the formula: Area of Sector = (α / 360°) × π r², where α is the central angle.
- 😀 The full angle of a circle is 360°, which helps in the formula for calculating the area of a sector.
- 😀 The formula for the area of a sector uses π, which can be approximated as 3.14 or 22/7.
- 😀 To apply the formula, first simplify the fraction of the central angle over 360°.
- 😀 An example calculation involves finding the area of a sector with a radius of 7 cm and a central angle of 120°.
- 😀 In the example, after simplifying the fraction (120°/360° = 1/3), the area is calculated as 51.33 cm².
- 😀 The formula to calculate the area of a sector relies on the proportion of the central angle relative to the full circle (360°).
- 😀 Practice problems are essential to reinforce the understanding of sector area calculations and ensure mastery.
Q & A
What is a sector (juring) of a circle?
-A sector (juring) of a circle is a region within the circle that is bounded by two radii and one arc of the circle.
What elements define a sector in a circle?
-A sector in a circle is defined by two radii, which are straight lines from the center of the circle to the circumference, and one arc, which is the curved boundary between the two points on the circumference.
How do you calculate the area of a sector of a circle?
-To calculate the area of a sector, use the formula: Area of sector = (α/360°) × πr², where α is the central angle of the sector, and r is the radius of the circle.
What is the formula for the area of a full circle?
-The formula for the area of a full circle is: Area of circle = πr², where r is the radius of the circle.
What does the central angle (α) represent in a sector?
-The central angle (α) represents the angle formed at the center of the circle between the two radii that define the sector.
In the formula for the area of a sector, what does the term (α/360°) represent?
-The term (α/360°) represents the fraction of the total circle that is occupied by the sector, where α is the central angle of the sector and 360° is the total angle of a full circle.
What happens if the central angle of the sector is 360°?
-If the central angle of the sector is 360°, the sector becomes the entire circle, and its area will be equal to the full area of the circle, i.e., πr².
How do you simplify the formula for calculating the area of a sector?
-To simplify the formula, first divide the central angle (α) by 360° to get the fraction of the circle's area. Then multiply by πr² to calculate the sector's area.
What is the solution to the example problem where the radius is 7 cm and the central angle is 120°?
-In this example, the area of the sector is calculated as follows: Area = (120°/360°) × (22/7) × 7² = 51.33 cm².
Why do we use both 22/7 and 3.14 for the value of π in calculations?
-Both 22/7 and 3.14 are approximations of the value of π. 22/7 is often used for simpler fractions in calculations, while 3.14 is a decimal approximation commonly used for ease of calculation.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)