MATRIKS RUANG VEKTOR | OPERASI BARIS ELEMENTER (OBE), MATRIKS ESELON BARIS TEREDUKSI
Summary
TLDRThis video tutorial focuses on understanding elementary row operations, which are essential tools for solving systems of linear equations. The video covers three types of operations: row swapping, multiplying a row by a non-zero constant, and adding a multiple of one row to another. These techniques help simplify matrices, making systems of equations easier to solve. The tutorial emphasizes the importance of mastering these operations for advancing in matrix theory and vector spaces. It also explores key properties of matrices, including row echelon form and reduced row echelon form, with practical examples to clarify their applications.
Takeaways
- 😀 Elemental row operations (OBE) are essential techniques for simplifying systems of linear equations to make them easier to solve.
- 😀 There are three main types of row operations: row swapping, multiplying a row by a non-zero constant, and adding a multiple of one row to another.
- 😀 Row swapping involves exchanging entire rows in a matrix to achieve the desired result, such as changing a leading entry to 1.
- 😀 Multiplying a row by a non-zero constant is used to scale rows, for example, converting a leading coefficient into 1 by multiplying by a constant.
- 😀 The addition of a multiple of one row to another is used to eliminate elements in a column, making the system simpler.
- 😀 A matrix's row echelon form (REF) and reduced row echelon form (RREF) can be achieved by performing these row operations to meet certain conditions.
- 😀 In the row echelon form, each row's leading 1 must appear further to the right as you move down the rows, and any row with all zeros should be at the bottom.
- 😀 In the reduced row echelon form, each column containing a leading 1 must have zeros in all other positions, ensuring that the matrix is fully reduced.
- 😀 Understanding and mastering row operations is crucial for progressing in matrix and vector space courses, as they are foundational tools for solving linear systems.
- 😀 Examples of matrices in row echelon and reduced row echelon forms illustrate the importance of row operations in transforming matrices into simpler forms for easier solution finding.
Q & A
What is the purpose of elementary row operations (ERO)?
-The purpose of elementary row operations is to simplify a system of linear equations by transforming the given system into a new system that has the same solution set but is easier to solve.
What are the three types of elementary row operations?
-The three types of elementary row operations are: 1) Row swapping (exchanging two rows), 2) Scalar multiplication (multiplying a row by a non-zero constant), and 3) Row addition (adding a scalar multiple of one row to another row).
Why is it important to understand elementary row operations in matrix and vector space courses?
-Understanding elementary row operations is crucial because they are foundational techniques for solving systems of linear equations, and they support more advanced concepts and operations in linear algebra.
Can we multiply a row by zero in elementary row operations?
-No, multiplying a row by zero is not allowed in elementary row operations because it would result in a row of zeros, which would violate the non-zero constant rule for scalar multiplication.
What happens when you swap two rows in a matrix?
-Swapping two rows in a matrix exchanges all the elements of the two rows. This operation helps in achieving desired matrix properties, such as simplifying a system of linear equations.
How does scalar multiplication work in elementary row operations?
-Scalar multiplication involves multiplying all elements of a row by a non-zero constant. For example, multiplying the first row of a matrix by 1/2 will divide each element of the row by 2.
What does 'row addition' mean in the context of elementary row operations?
-Row addition involves adding a scalar multiple of one row to another row. This operation is used to modify a row while keeping the overall system of equations equivalent.
What is the significance of the 'leading 1' in a row echelon form matrix?
-In row echelon form, the leading entry (or 'leading 1') in each row should be 1, and it should be to the right of the leading entry in the row above. This makes it easier to solve the system of equations using back substitution.
What is the difference between row echelon form and reduced row echelon form?
-In row echelon form (REF), each leading entry is 1 and the entries below it are zeros, but the entries above the leading 1 are not necessarily zeros. In reduced row echelon form (RREF), in addition to the conditions for REF, each leading 1 must also have zeros above it.
How do you know if a matrix is in row echelon form or reduced row echelon form?
-A matrix is in row echelon form (REF) if it satisfies the conditions of having leading 1's that move to the right in each successive row, with zeros below the leading 1's. It is in reduced row echelon form (RREF) if, in addition to the REF conditions, all entries above each leading 1 are also zero.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Introduction to SLE
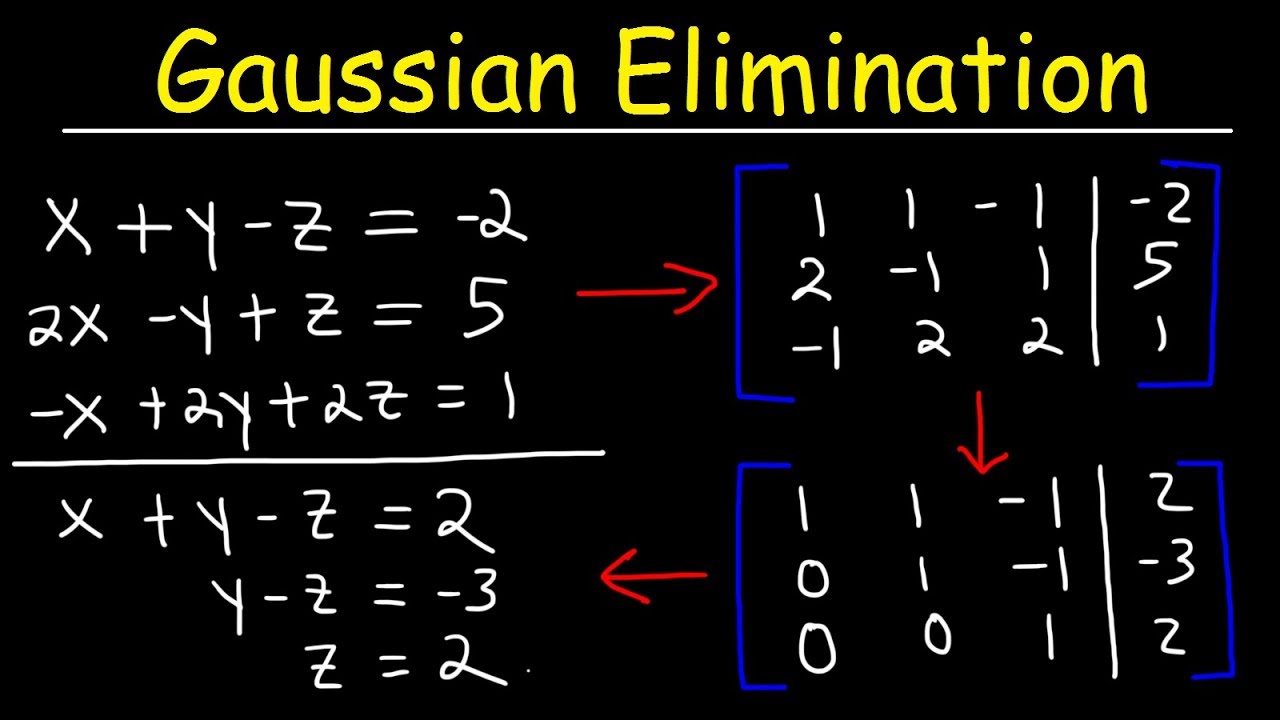
Gaussian Elimination & Row Echelon Form
Linear equations Gaussian Methods - English

Imagen, kernel (o espacio nulo), rango, nulidad, espacio columna y espacio fila de una matriz.
Gaussian elimination | Lecture 10 | Matrix Algebra for Engineers

Common Core Algebra II.Unit 3.Lesson 7.Systems of Linear Equations
5.0 / 5 (0 votes)