Peluang Kejadian Saling Lepas dan Kejadian Saling Bebas

Summary

This video delves into probability concepts, specifically focusing on mutually exclusive, independent, and dependent events. The presenter explains key concepts like mutually exclusive events that cannot occur together (e.g., rolling an odd or even number on a die), and independent events where one event doesn't affect another (e.g., rolling a die twice). The video includes practical examples, such as rolling dice, drawing cards, and picking balls without replacement, to help viewers understand how to calculate probabilities using appropriate formulas. It’s a helpful guide for those looking to strengthen their grasp on basic probability principles.

Takeaways

• 😀 The script explains the concept of mutually exclusive events, where two events cannot occur simultaneously, using examples such as rolling a die and the occurrence of odd or even numbers.
• 😀 The formula for calculating the probability of mutually exclusive events is shared: P(A ∪ B) = P(A) + P(B).
• 😀 An example involving a die and the calculation of probabilities for odd and even outcomes is presented, resulting in a probability of 4/6 for either outcome.
• 😀 The script also explains the concept of mutually inclusive events, where two events can happen together, illustrated by the example of rolling a die and getting either an even number or a multiple of 3.
• 😀 The formula for calculating the probability of mutually inclusive events is provided: P(A ∪ B) = P(A) + P(B) - P(A ∩ B), where the intersection is subtracted to avoid double-counting.
• 😀 An example using a deck of cards is given to illustrate mutually inclusive events, such as drawing an Ace or a Diamond. The script explains how to calculate this probability by considering overlapping events.
• 😀 The concept of independent events is introduced, where the occurrence of one event does not affect the probability of another, with examples like tossing two dice.
• 😀 The formula for independent events is explained: P(A ∩ B) = P(A) × P(B), which reflects that the two events do not influence each other.
• 😀 An example involving rolling a die twice is given, where the probability of getting a value less than 4 on the first roll and greater than 4 on the second roll is calculated using the independent event formula.
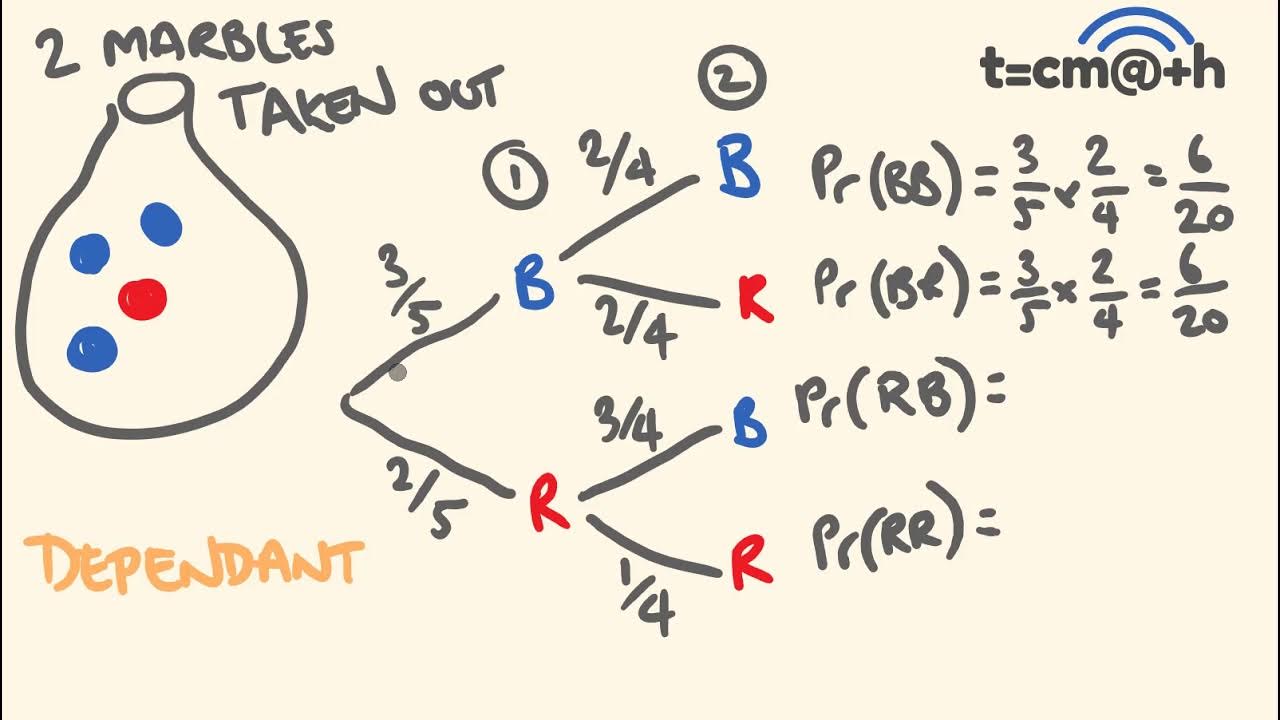
• 😀 The script discusses dependent events, where the outcome of one event influences the probability of subsequent events. An example is given with drawing balls from a box without replacement, changing the total number of available balls for each draw.

Q & A

What are mutually exclusive events in probability?

Mutually exclusive events are events that cannot occur at the same time. For example, when rolling a die, getting an odd number and getting an even number are mutually exclusive events because both cannot happen on the same roll.

Can you provide an example of mutually exclusive events in probability?

An example is rolling a die and getting either an odd or even number. Since a die cannot land on both an odd and even number at the same time, these two events are mutually exclusive.

What formula is used to calculate the probability of mutually exclusive events?

The formula used to calculate the probability of mutually exclusive events is P(A ∪ B) = P(A) + P(B), where A and B are mutually exclusive events. The probability of both events happening together is zero, hence we simply add the probabilities.

What are non-mutually exclusive events in probability?

Non-mutually exclusive events are events that can occur together. For example, when rolling a die, the event of rolling an even number and the event of rolling a multiple of 3 can occur together if you roll a 6.

How do you calculate the probability of non-mutually exclusive events?

The formula for non-mutually exclusive events is P(A ∪ B) = P(A) + P(B) - P(A ∩ B). This accounts for the overlap between the events, ensuring we don't double-count the outcomes where both events occur.

What is the definition of independent events in probability?

Independent events are events where the outcome of one event does not affect the outcome of another event. For example, when rolling two dice, the result of the first die does not affect the result of the second die.

Can you give an example of independent events in probability?

An example of independent events is flipping a coin twice. The result of the first flip (either heads or tails) does not influence the result of the second flip.

What formula do you use for independent events in probability?

For independent events, the probability of both events happening is calculated as P(A ∩ B) = P(A) * P(B), meaning the probability of both events occurring is the product of their individual probabilities.

What are non-independent events in probability?

Non-independent events are events where the outcome of one event affects the probability of the other event. For example, drawing balls from a box without replacement affects the probabilities of subsequent draws.

How does the probability change for non-independent events like drawing balls without replacement?

In non-independent events like drawing balls without replacement, the probability changes because after each draw, the total number of possible outcomes decreases, thus altering the probability of future events.