Geometría Analítica: División de segmento en tres en una razón dada
Summary
TLDREn este video, se resuelve un problema de geometría sobre la división de un segmento en tres partes iguales. Se describe cómo calcular las coordenadas de los puntos de división utilizando la fórmula de división de segmentos. Se explica cómo aplicar la razón de división, eligiendo correctamente la orientación de los puntos y utilizando fórmulas para obtener las coordenadas exactas. El enfoque está en la importancia de los cálculos precisos y la correcta aplicación de las fórmulas en geometría, con énfasis en la comprensión de la razón de división y su relación con las coordenadas.
Takeaways
- 😀 El problema consiste en dividir un segmento entre dos puntos en tres partes iguales.
- 😀 Los puntos extremos del segmento están en las coordenadas A(-3, y1) y B(4, 3).
- 😀 Se requiere encontrar las coordenadas de los dos puntos de división en el segmento.
- 😀 Para dividir el segmento en tres partes iguales, utilizamos el concepto de razón de división.
- 😀 La orientación del segmento, ya sea de A a B o viceversa, es crucial para aplicar la fórmula correctamente.
- 😀 Se utiliza la fórmula de la división de segmentos para hallar las coordenadas de los puntos de división.
- 😀 Para el primer punto de división, la razón es 1:2, lo que significa que el punto está más cerca de A.
- 😀 El cálculo de las coordenadas de un punto de división utiliza la fórmula de la sección, que toma en cuenta las coordenadas de los extremos y la razón de división.
- 😀 El primer punto de división tiene las coordenadas aproximadamente (2, -1).
- 😀 El segundo punto de división se calcula usando la razón 2:1 y tiene las coordenadas aproximadamente (3, 1).
- 😀 Los cálculos son importantes para obtener las coordenadas exactas, aunque un diagrama visual puede ayudar a entender mejor la división.
Q & A
¿De qué trata el problema presentado en el video?
-El problema trata sobre la división de un segmento en tres partes iguales, dado un segmento con extremos en los puntos P(-3, 4) y Q(4, 3). Se pide encontrar las coordenadas de los puntos de división.
¿Cuántos puntos de división se necesitan en este problema?
-Se necesitan dos puntos de división, ya que el segmento debe ser dividido en tres partes iguales.
¿Cómo se determina la posición de los puntos de división?
-Se usa la fórmula de división de segmentos para calcular las coordenadas de los puntos de división, tomando en cuenta la razón de división entre los puntos.
¿Cuál es la razón de división utilizada en el problema?
-La razón de división es 1:2, porque el segmento se divide en tres partes iguales, y cada punto divide el segmento en una proporción de 1 a 2.
¿Qué fórmula se utiliza para calcular las coordenadas de los puntos de división?
-Se utiliza la fórmula de la división de segmentos en una razón m:n: X = (m * x2 + n * x1) / (m + n), Y = (m * y2 + n * y1) / (m + n).
¿Qué diferencia existe entre la división de la primera y la segunda parte del segmento?
-Para la primera parte, la razón de división es 1:2, y para la segunda parte, la razón de división es 2:1, ya que la segunda división toma los puntos restantes del segmento.
¿Por qué es importante la orientación de los puntos P y Q?
-La orientación de los puntos P y Q es importante porque determina el orden en que se aplican las fórmulas para calcular las coordenadas de los puntos de división, lo que afecta el resultado final.
¿Cómo se seleccionan las coordenadas iniciales y finales para usar la fórmula de división?
-Las coordenadas iniciales y finales se seleccionan de acuerdo con la orientación elegida, es decir, si se elige dividir el segmento de P a Q, las coordenadas de P y Q serán las que se utilicen en la fórmula.
¿Qué coordenadas tiene el primer punto de división M?
-El primer punto de división M tiene coordenadas aproximadas de (-0.67, 3.67).
¿Cómo se calcula la coordenada de Y para el punto de división M?
-La coordenada de Y para el punto de división M se calcula utilizando la fórmula: Y_M = (1 * 3 + 2 * 4) / (1 + 2), lo que da un resultado aproximado de 3.67.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

25. Punto que divide a un segmento en una razón, EXPLICACION COMPLETA

Geometría Analítica: Circunferencia y dos punto detecta un error de cálculo.

Fracciones en la recta numérica
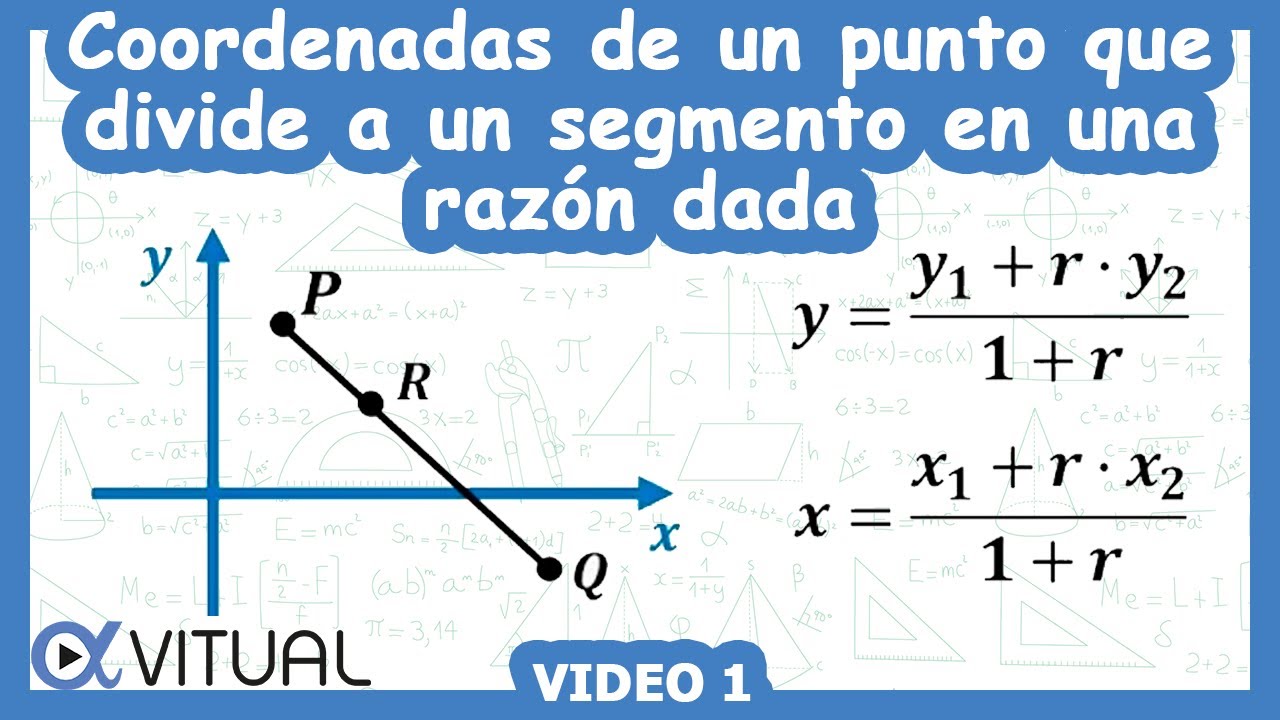
Coordenadas de un punto que divide a un segmento en una razón dada ejemplo 1 | Geometría - Vitual
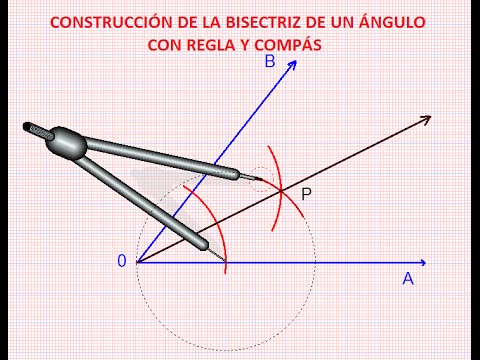
CONSTRUCCIÓN DE LA BISECTRIZ DE UN ANGULO CON REGLA Y COMPÁS

Definición de vector - MATEMÁTICAS
5.0 / 5 (0 votes)
