ANALISA STRUKTUR 2 MATRIKS FLEKSIBILITAS SOAL & PEMBAHASAN#Matriksfleksibilitas#Flexibilitymatrix
Summary
TLDRIn this video, the speaker provides an in-depth explanation of the matrix method, specifically focusing on the flexibility method for analyzing continuous beams in structural engineering. The video walks through the process of calculating reactions, moments, and deflections of a beam subjected to both uniformly distributed and point loads. By breaking down the problem into manageable steps, the speaker demonstrates how to construct the flexibility matrix, apply unit forces, and determine the final structural response. The tutorial aims to help viewers better understand the core principles of structural analysis through practical application and detailed examples.
Takeaways
- 😀 The video discusses the matrix method for structural analysis, focusing on continuous beams.
- 😀 The structure is a continuous beam with two segments: AB and BC, with various loads applied.
- 😀 The first step is to determine the reactions at the supports of the beam (AB and C).
- 😀 The second step involves splitting the continuous beam into two segments for easier analysis of moments in each part.
- 😀 The beam AB is subjected to a uniform load, and the maximum moment occurs at the center, while BC experiences a concentrated load with its maximum moment at the midpoint.
- 😀 The moments for each segment are calculated using standard formulas, with the results indicating the type of load (uniform or concentrated).
- 😀 The third step involves converting the calculated moments into equivalent forces to evaluate deflection.
- 😀 The fourth step is to determine the reactions at the supports using the equivalent forces for each beam segment.
- 😀 The matrix flexibility method is used in step five to assemble the flexibility matrix for the structure, which is essential for analyzing displacement.
- 😀 The process includes applying unit forces to the reactions and calculating the resulting bending moments in the structure.
- 😀 The final output includes the bending moment diagram and the calculation of deflections and moments, providing a comprehensive understanding of the beam’s behavior under load.
Q & A
What is the main focus of the video script?
-The video focuses on explaining the matrix method (also known as the Flexibility Method) for solving continuous beam problems in civil engineering. It involves calculating reactions, moments, and deflections in a structure.
What type of structure is being analyzed in the example?
-The structure being analyzed is a continuous beam with two spans, labeled AB and BC. The beam has specific loads, including a uniformly distributed load and a concentrated point load.
What are the main loads applied to the beam in the example?
-The beam experiences a uniformly distributed load of 60 kN/m on span AB, and a concentrated point load of 100 tons at point B.
What are the steps involved in solving the beam problem using the matrix method?
-The steps include: 1) Determining the reactions at the supports, 2) Describing the structure and calculating the moments at points of interest, 3) Converting moments to equivalent loads, 4) Calculating the reactions at supports based on these loads, 5) Determining the flexibility matrix, and 6) Using the flexibility method to find deflections and moments.
How is the moment at the middle of a span (M_AB) calculated for a uniformly distributed load?
-The moment for a uniformly distributed load (M_AB) is calculated using the formula: M_AB = WL^2 / 8, where W is the load intensity and L is the span length.
How is the moment (M_BC) calculated for a concentrated point load?
-The moment (M_BC) for a concentrated point load is calculated using the formula: M_BC = PL / 4, where P is the point load and L is the length of the span.
What role do the reactions at the supports play in the matrix method?
-The reactions at the supports are essential for determining the internal forces and moments in the beam. These reactions help in constructing the flexibility matrix and calculating the beam's deflections and moments.
What is the significance of the flexibility matrix in the solution?
-The flexibility matrix represents the relationship between applied forces and resulting displacements in the structure. It is used to compute deflections and internal moments based on the applied loads and boundary conditions.
How are the deflections at various points calculated using the matrix method?
-Deflections are calculated by solving the system of equations derived from the flexibility matrix. The displacements are related to the forces using the equation Δ = F * α, where F is the force vector and α is the flexibility matrix.
How does the method handle different types of loads (uniform and point loads)?
-The method treats uniform and point loads differently by applying specific formulas for moments. For uniform loads, the moment distribution is parabolic, while for point loads, the moment distribution is triangular, with the maximum moment occurring at the point of application.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

ANALISA STRUKTUR 2 KONSEP DASAR MATRIKS FLEKSIBILITAS#flexibilitymatrix#Flexibility#matrix

Beban Terfaktor (Ultimate Load) dan Kuat Rencana (Design Strength) Struktur Baja | Lightboard

ANALISA STRUKTUR 2 MATRIKS KEKAKUAN LANGSUNG BALOK SOAL&PEMBAHASAN#Stiffnessglobalmatrix#matrix
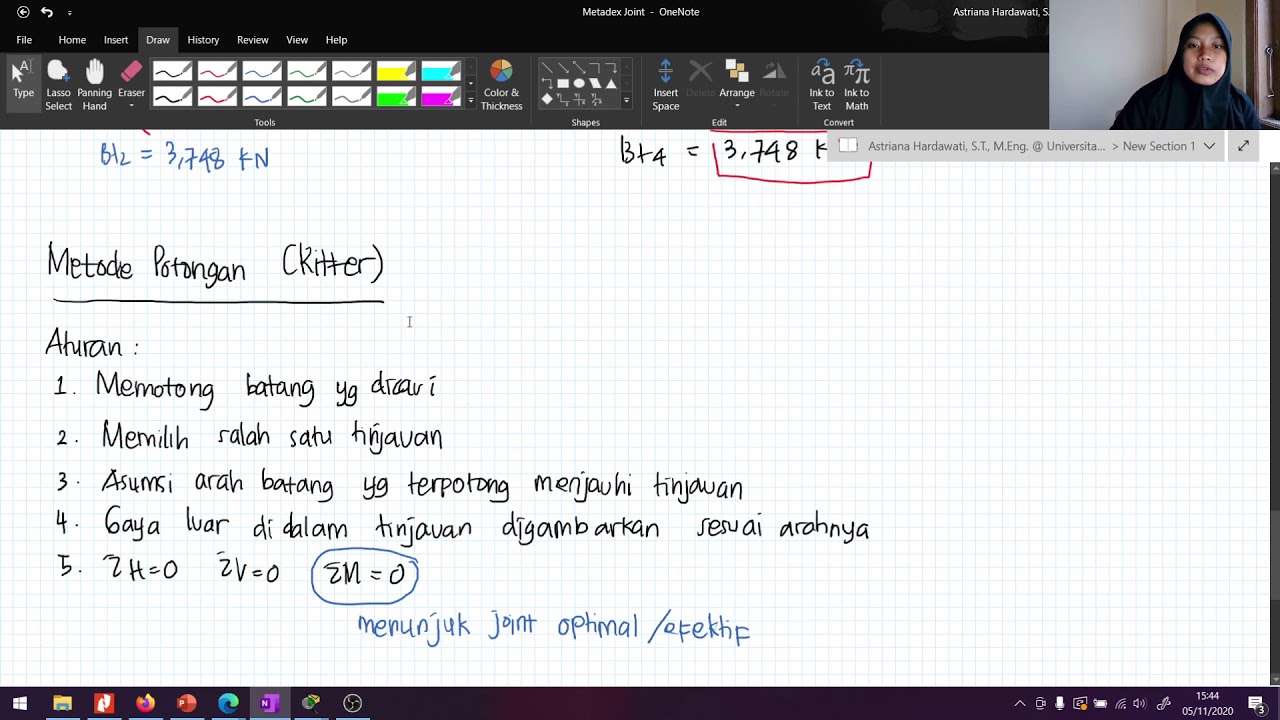
Statika 1 Metode Potongan (1)
SA21: Virtual Work Method (Trusses)

Video #4 Balok Kantilever
5.0 / 5 (0 votes)