HUKUM BERNOULLI | Fluida Bergerak - Fisika Kelas 11
Summary
TLDRIn this educational video, the instructor explains Bernoulli's Law, a fundamental concept in fluid dynamics. The law states that an increase in the speed of a fluid results in a decrease in pressure. Through demonstrations, such as blowing air between two pieces of paper, the instructor illustrates how pressure differences create movement. The video also covers the Bernoulli equation, used to calculate fluid behavior in pipes and other systems, and explores practical applications like air travel and water pumps. The lesson is further enriched with example problems, allowing viewers to understand and apply these principles to real-world scenarios.
Takeaways
- 😀 Bernoulli's principle explains that when the speed of a fluid increases, its pressure decreases, and vice versa.
- 😀 The principle is demonstrated with a simple experiment using two pieces of paper and blowing air between them, showing that higher speed results in lower pressure.
- 😀 Bernoulli's principle applies to both air and water (fluids) and is key to explaining how airplanes fly, as differences in airspeed create lift.
- 😀 Bernoulli's equation is derived from the conservation of mechanical energy, incorporating pressure, kinetic energy, and potential energy of the fluid.
- 😀 Bernoulli's equation for a moving fluid is given as: P1 + ½ρV1² + ρgh1 = P2 + ½ρV2² + ρgh2, where P is pressure, ρ is fluid density, V is velocity, g is gravity, and h is height.
- 😀 The equation can be used to calculate pressure differences in systems such as water pumping, where a pump creates pressure to move water from a lower to a higher elevation.
- 😀 In practical applications, Bernoulli's equation helps determine the required pressure for water to reach specific heights in systems like water towers.
- 😀 The concept of continuity applies when calculating the velocity of fluid in pipes with different cross-sectional areas, as fluid velocity increases when the pipe narrows.
- 😀 In a horizontal pipe, when the fluid speed changes, Bernoulli's equation helps determine the pressure difference between two points.
- 😀 Example calculations illustrate how Bernoulli's equation can be used to determine the required pressure to maintain fluid flow in real-world applications like plumbing or aircraft design.
Q & A
What is Bernoulli's Principle and how does it relate to fluid dynamics?
-Bernoulli's Principle states that in a moving fluid, an increase in the speed of the fluid results in a decrease in pressure. This relationship shows that when a fluid flows faster, its pressure is lower, and when it flows slower, its pressure is higher.
Can you explain the basic concept of Bernoulli’s principle with a real-life example?
-A simple example to demonstrate Bernoulli's principle is the behavior of two pieces of paper held apart. When air is blown between them, the air moves faster in the middle, creating lower pressure. The higher pressure outside the papers pushes them together, illustrating the principle.
How does Bernoulli's Principle explain how an airplane achieves lift?
-An airplane's wings are designed so that the air moves faster over the top surface than under the bottom. According to Bernoulli's Principle, the faster-moving air over the top creates lower pressure, and the higher pressure below the wings pushes the airplane upward, generating lift.
What are the components of the Bernoulli equation?
-The Bernoulli equation is a statement of the conservation of energy for flowing fluids. It involves three terms: pressure energy (P), kinetic energy (1/2 * ρ * v^2), and potential energy (ρ * g * h), where ρ is fluid density, v is velocity, g is gravitational acceleration, and h is height.
How can Bernoulli’s equation be used to calculate the pressure difference in a fluid system?
-Bernoulli’s equation can be rearranged to solve for the pressure difference between two points in a fluid system by accounting for differences in height and velocity. The formula is: P1 + (1/2 * ρ * v1^2) + ρ * g * h1 = P2 + (1/2 * ρ * v2^2) + ρ * g * h2.
How does Bernoulli’s principle apply to the flow of water in pipes with varying diameters?
-When water flows through pipes with varying diameters, Bernoulli’s principle shows that where the pipe is narrower, the water flows faster, which results in lower pressure. Conversely, in wider sections of the pipe, the flow slows down and the pressure increases.
What happens when water is pumped from a lower to a higher elevation, and how does Bernoulli’s equation describe this?
-When water is pumped to a higher elevation, the pressure increases at the lower point of the pipe to overcome the gravitational potential energy. Bernoulli's equation can help calculate the pressure required to move water to a higher elevation by factoring in changes in velocity and height.
In what real-world applications is Bernoulli’s principle used?
-Bernoulli’s principle is used in a variety of applications, including explaining how airplanes achieve lift, designing efficient fluid transport systems (such as water pipes), and understanding the behavior of fluids in various engineering systems like pumps and turbines.
What is the significance of fluid density in Bernoulli’s equation?
-Fluid density (ρ) plays a key role in Bernoulli’s equation as it affects both the kinetic and potential energy terms. A higher fluid density increases the pressure required to move the fluid and impacts how energy is distributed across the system.
How can Bernoulli’s equation be used to determine the speed of fluid flow in a pipe?
-By applying Bernoulli’s equation along with the continuity equation (which conserves mass), you can determine the speed of fluid flow in different parts of a pipe by comparing cross-sectional areas and pressure differences between points in the system.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Penerapan Prinsip Bernoulli Dalam Kehidupan Sehari-Hari

MekFlu #1: Prinsip Persamaan Bernoulli
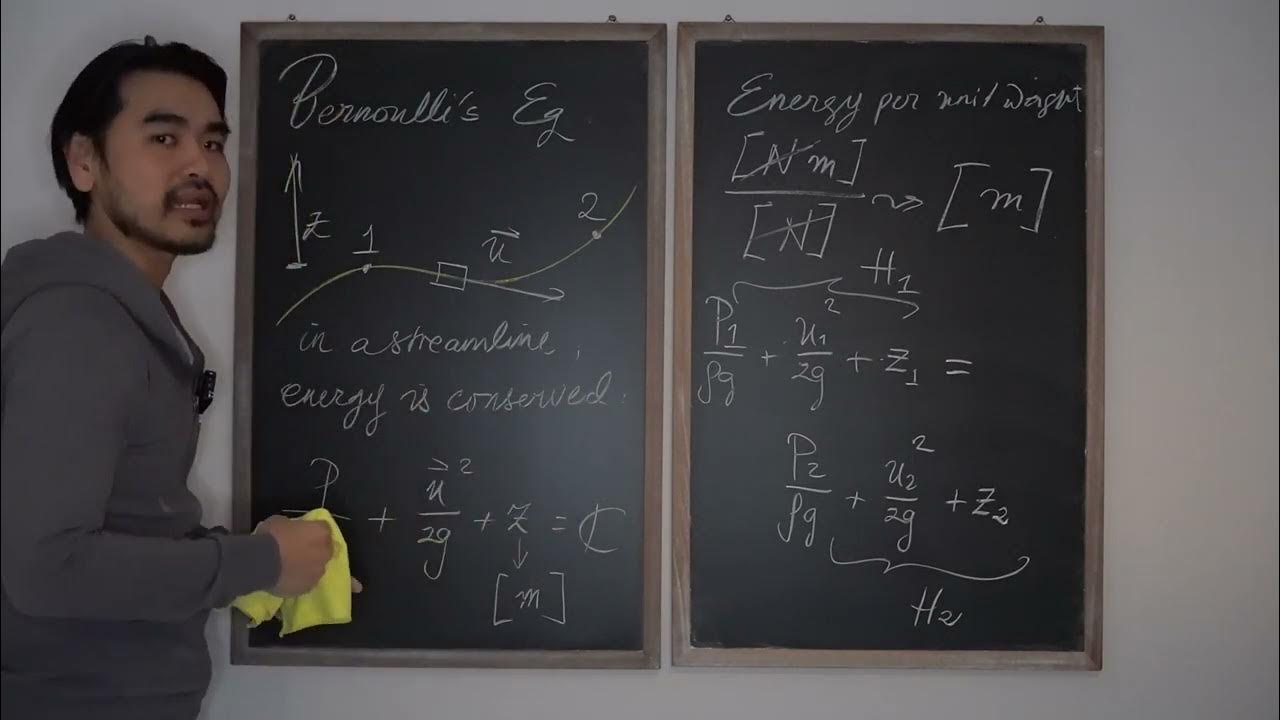
Mekanika Fluida FM01 (Lecture3: 1/8). Persamaan Bernoulli (Pengenalan)

MekFlu #2: Persamaan Bernoulli, Kontinuitas dan Kekekalan Energi

Dinamika Fluida

Mekanika Fluida FM01 (Lecture3: 8/8). Energy Line & Hydraulic Grade Line
5.0 / 5 (0 votes)