9 Deflection Test

Summary

This video explains a procedure to measure the modulus of elasticity of a beam using concentrated loads and deflection. The process involves applying a load at the midpoint of a beam, measuring its deflection, and using the formula Δ = WL³ / 48EI to calculate the modulus of elasticity. The experiment includes plotting a graph of load vs. deflection to determine the value for W/Δ. Additionally, the video covers different loading conditions and methods for verifying results, providing an in-depth understanding of material behavior under load.

Takeaways

• 😀 The experiment aims to measure the modulus of elasticity of a beam through deflection analysis.
• 😀 A loaded fan, weights, a graduated scale, and a wooden specimen are required for the setup.
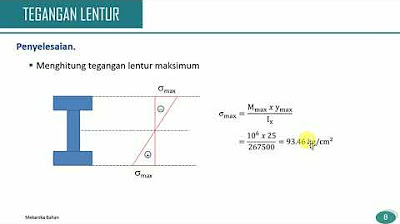
• 😀 The deflection formula is given by Delta = WL^3 / 48EI, where W is the load, L is the span, E is the modulus of elasticity, and I is the moment of inertia.
• 😀 The moment of inertia is calculated using the formula I = BD^3 / 12, where B is the beam's width and D is the depth.
• 😀 The span of the beam (L) is fixed for the experiment and can be measured using a scale.
• 😀 The experiment involves applying a concentrated load at the midpoint of the beam and measuring deflection.
• 😀 The modulus of elasticity is calculated using the formula E = WL^3 / 48I * (1 / Delta).
• 😀 The procedure involves incrementally adding weights and measuring the deflection at each step.
• 😀 A graph of load vs. deflection is plotted, which should result in a straight-line graph.
• 😀 The slope of the load vs. deflection graph is used to calculate W / Delta, which helps determine the modulus of elasticity.
• 😀 A similar procedure can be applied for central loading, where the deflection formula changes to Delta = W a^2 B^2 / 3EI.

Q & A

What is the main principle behind the deflection of beams under load in this experiment?

The main principle is that when a concentrated load is applied at the midpoint of a beam, it causes deflection, which can be calculated using the formula Delta = WL^3 / 48EI, where W is the load, L is the span, E is the modulus of elasticity, and I is the moment of inertia of the beam.

What does the formula Delta = WL^3 / 48EI represent in this experiment?

This formula represents the deflection (Delta) of a beam under a concentrated load. W is the load applied, L is the span of the beam, E is the modulus of elasticity, and I is the moment of inertia of the beam.

How is the moment of inertia (I) of the beam calculated?

The moment of inertia (I) is calculated using the formula I = BD^3 / 12, where B is the width of the beam and D is its depth, which can be measured using a scale.

What is the role of the span (L) in the deflection calculation?

The span (L) refers to the distance between the supports of the beam, and it plays a critical role in the deflection calculation. A larger span increases the deflection, as seen in the WL^3 term of the deflection formula.

What does the term 'modulus of elasticity' (E) signify in the context of this experiment?

The modulus of elasticity (E) is a material property that indicates the stiffness of the material. In this experiment, it is used to determine the deflection of the beam under a given load.

How do you measure the deflection of the beam in this experiment?

The deflection is measured using a graduated scale placed at the mid-point of the beam. The deflection is recorded at different load increments, and the results are used to plot a graph.

What is the purpose of plotting a graph between load and deflection?

The purpose of plotting a graph between load and deflection is to visually analyze the relationship between the load applied to the beam and its deflection. The slope of the graph can then be used to calculate the modulus of elasticity.

What does the slope of the load-deflection graph represent?

The slope of the load-deflection graph represents the ratio W/Delta. This ratio is used to calculate the modulus of elasticity (E) of the beam.

What is the significance of conducting the experiment for both central and non-central loading?

Conducting the experiment for both central and non-central loading allows the verification of the deflection formulas for different loading scenarios. For non-central loading, the formula for deflection changes to Delta = W a^2 b^2 / 3EI.

What is the theoretical basis for the deflection equivalence when the load is applied at two different points?

The theoretical basis is that when a load is applied at point A and the deflection at point B is measured, and vice versa, the deflections must be equal. This is known as the reciprocal deflection theorem, which can be verified by applying the respective formulas for deflection.