GEOMETRIA PLANA: SOMA DOS ÂNGULOS INTERNOS (α + β) #IF2021
Summary
TLDRIn this educational video, the instructor explains how to solve a geometry problem involving the angles Alpha (α) and Beta (β) in a quadrilateral. Using the properties of supplementary angles and the fact that the sum of interior angles in a quadrilateral is 360°, the teacher guides viewers through the steps to find that the sum of α and β equals 130°. The video offers clear, step-by-step instructions, practical tips, and emphasizes essential concepts to help viewers solve similar angle-related problems with ease.
Takeaways
- 😀 The problem involves determining the sum of two unknown angles, Alpha + Beta, with given alternatives.
- 😀 The first key concept discussed is **supplementary angles**, where two angles on a straight line add up to 180°.
- 😀 The speaker explains that to find an unknown angle when one is known (e.g., 30°), simply subtract the known angle from 180° (180° - 30° = 150°).
- 😀 The sum of the internal angles of any quadrilateral is 360°, which is an important principle used to solve the problem.
- 😀 The speaker uses the geometry of a quadrilateral with one known angle (40°) to set up an equation to find the sum of Alpha and Beta.
- 😀 The equation for the sum of Alpha and Beta is formed by subtracting known angles from the total sum of 360°.
- 😀 The speaker walks through the algebraic steps to solve the equation, demonstrating how to isolate the unknown angles (Alpha and Beta).
- 😀 After simplifying the equation, the sum of Alpha + Beta is found to be 130°.
- 😀 The video encourages viewers to leave feedback and engage with the content by liking and sharing the video.
- 😀 The lesson highlights the importance of understanding basic geometric principles like supplementary angles and angle sums in polygons.
- 😀 The speaker offers two helpful tips for solving geometry problems related to angle sums and relationships.
Q & A
What is the sum of the interior angles of a quadrilateral?
-The sum of the interior angles of a quadrilateral is always 360°.
What geometric principle does the speaker use to calculate unknown angles?
-The speaker uses the principle that the sum of the interior angles of a quadrilateral is 360°, and also applies the concept of supplementary angles (where two angles add up to 180°).
How do supplementary angles help in solving for Alpha and Beta?
-Supplementary angles help because they are angles that add up to 180°. By subtracting known angles from 180°, the speaker calculates the unknown angles Alpha and Beta.
What is the first tip provided by the speaker for solving these types of problems?
-The first tip is that the sum of the interior angles of any figure with four sides (such as a quadrilateral) is 360°.
What is the second tip provided by the speaker?
-The second tip is that supplementary angles, which add up to 180°, can be used to calculate the value of the unknown angles in the problem.
How does the speaker simplify the equation for finding Alpha + Beta?
-The speaker simplifies the equation by first using the sum of angles in a quadrilateral (360°) and subtracting known angles from 180° to find the unknown angles. The final equation simplifies to 130° for the sum of Alpha and Beta.
What was the specific value for the sum of Alpha and Beta?
-The sum of Alpha and Beta was determined to be 130°.
What mathematical operation is used to calculate the unknown angle if one angle is known?
-The operation used is subtraction: 180° minus the known angle is used to find the unknown supplementary angle.
What happens when the equation is simplified after applying the principles?
-After applying the principles, the equation simplifies to 130°, which is the sum of Alpha and Beta, and matches one of the provided answer choices.
What is the role of the angle of 40° in the problem-solving process?
-The 40° angle is one of the known angles in the quadrilateral. It is used in the calculation along with the supplementary angle principle to find the unknown angles Alpha and Beta.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
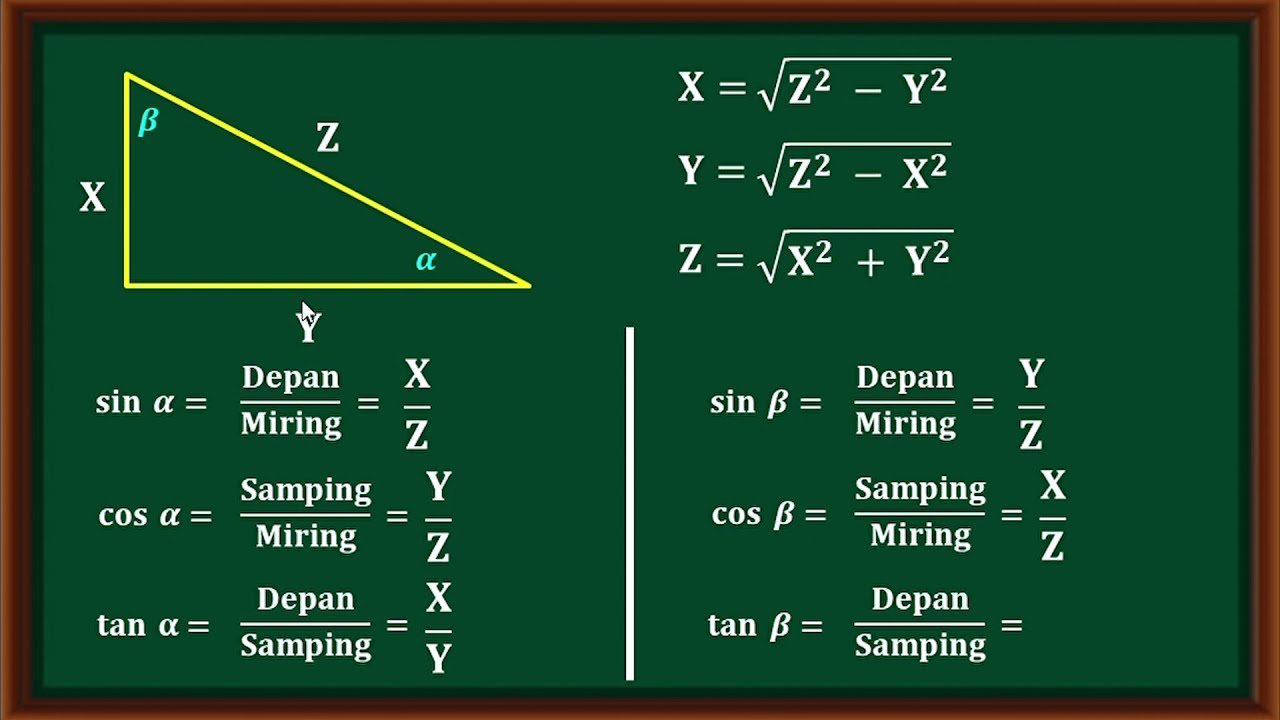
Materi dan soal pembahasan Perbandingan trigonometri dari suatu sudut pada segitiga siku-siku.
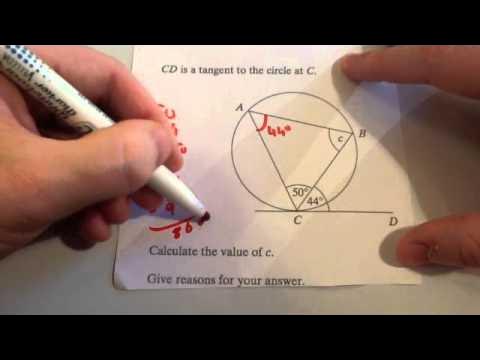
Circle Theorems questions - Corbettmaths
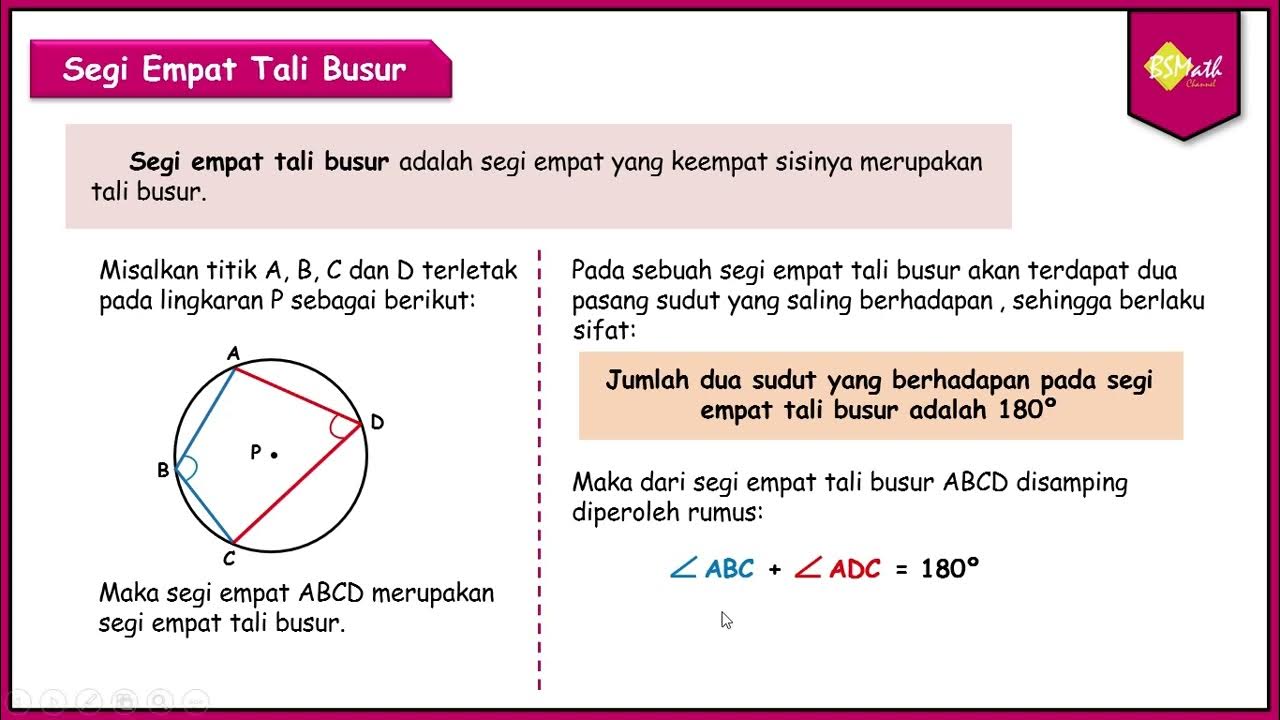
Segi Empat Tali Busur Lingkaran - Matematika SMA Kelas XI Kurikulum Merdeka

Lingkaran [Part 2] - Sudut Pusat dan Sudut Keliling

Grade 9 Mathematics, Quarter 3 Module 1: Quadrilaterals and Parallelograms

Angle Properties of Quadrilaterals
5.0 / 5 (0 votes)