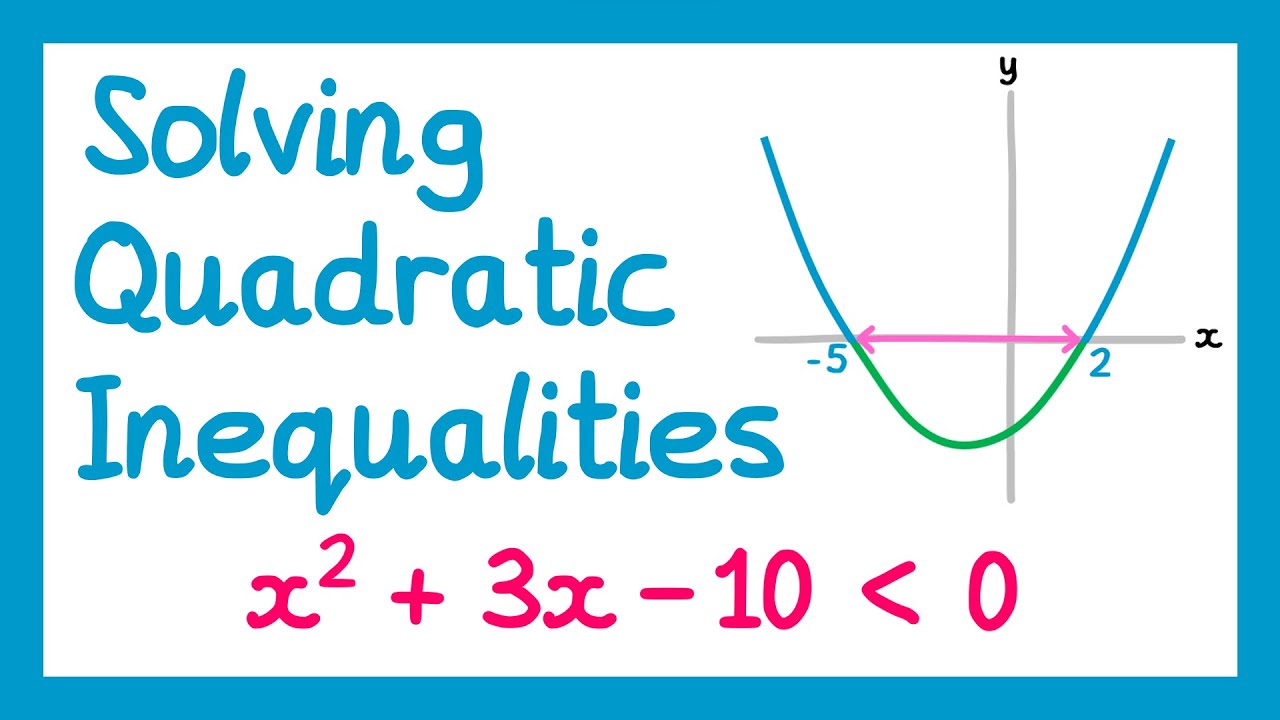2a) Quadratic inequalities grade 11 | Try

Summary

In this video, the speaker explains the steps to solve an inequality involving a quadratic equation, x² - 6x - 7 > 0. The process includes factoring, drawing a timeline, and analyzing the parabola to determine where the graph is greater than zero. The video outlines two methods for solving the inequality, including a number line approach and testing intervals within the solution. The final answer shows that x must be less than -1 or greater than 7. The speaker also offers alternative methods and explains interval notation for a clearer understanding of the solution.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

Q & A

What is the first step in solving the inequality presented in the transcript?

The first step is to move all terms to one side of the inequality. This results in the expression x^2 - 6x - 7.

What is the mistake that students often make when trying to factorize the expression?

Students often incorrectly factorize the expression as (x - 7) > 0 or (x + 1) > 0, which is not correct.

How does the teacher suggest solving the inequality graphically?

The teacher suggests drawing a timeline and using a parabola to visualize the solution, which shows where the graph is above the x-axis (i.e., where the expression is greater than zero).

What does 'above the x-axis' mean in the context of this problem?

It means that the values of the parabola are positive, which corresponds to where the expression x^2 - 6x - 7 is greater than zero.

What are the two intervals where the inequality x^2 - 6x - 7 > 0 is satisfied?

The inequality is satisfied when x is less than -1 or when x is greater than 7.

What is the second method used to solve the inequality, as mentioned in the transcript?

The second method involves factoring the expression and then testing values from different intervals on a number line to determine where the expression is positive.

How does the teacher determine the sign of the expression in each interval?

The teacher selects a test point in each interval, substitutes it into the factored expression, and checks whether the result is positive or negative.

What values are tested in the different intervals?

In the interval less than -1, the teacher tests -2. In the interval between -1 and 7, the teacher tests 0. In the interval greater than 7, the teacher tests 8.

What is the significance of the test values in the second method?

The test values help determine the sign of the expression in each interval, allowing us to identify where the inequality is satisfied (where the expression is positive).

How can the solution to the inequality be expressed in interval notation?

The solution can be written in interval notation as (-∞, -1) ∪ (7, ∞), which indicates that x is either less than -1 or greater than 7.