5 - Class 12 - Chemistry - Solid State - Calculation of number of atoms per unit cell
Summary
TLDRThe transcript explains how to calculate the number of particles in a unit cell of a crystal lattice. It covers the contributions of different types of atoms based on their positions within the unit cell: corner atoms (1/8 contribution), face-centered atoms (1/2 contribution), body-centered atoms (full contribution), and edge-centered atoms (1/4 contribution). The script then provides examples for three types of crystal structures: simple cubic, body-centered cubic, and face-centered cubic, with each structure's total atom count calculated based on these contributions, resulting in 1, 2, and 4 atoms per unit cell, respectively.
Takeaways
- 😀 A crystal lattice consists of a large number of unit cells, each containing lattice points occupied by constituent particles.
- 😀 A constituent particle at a lattice point may be shared between multiple unit cells.
- 😀 A corner atom is shared by eight unit cells, contributing one-eighth of an atom to each unit cell.
- 😀 A face-centered atom is shared between two unit cells and contributes half an atom to each unit cell.
- 😀 A body-centered atom is not shared with other unit cells and contributes a full atom to its unit cell.
- 😀 An edge-centered atom is shared by four unit cells and contributes one-fourth of an atom to each unit cell.
- 😀 In a simple cubic unit cell, there are 8 corner atoms, each contributing one-eighth of an atom, totaling 1 atom per unit cell.
- 😀 In a body-centered cubic unit cell, there are 8 corner atoms and 1 body-centered atom, totaling 2 atoms per unit cell.
- 😀 In a face-centered cubic unit cell, there are 8 corner atoms and 6 face-centered atoms, totaling 4 atoms per unit cell.
- 😀 The number of atoms per unit cell varies depending on the type of cubic structure: simple cubic (1), body-centered cubic (2), and face-centered cubic (4).
Q & A
What is a unit cell in a crystal lattice?
-A unit cell in a crystal lattice is the smallest repeating structure that, when replicated, forms the entire lattice. It contains all the necessary information about the arrangement of particles within the lattice.
How are particles distributed in a unit cell?
-In a unit cell, every lattice point is occupied by a constituent particle, which may be shared by multiple adjacent unit cells depending on its location.
How does the position of a particle affect its contribution to the unit cell?
-The contribution of a particle to the unit cell depends on its position. For example, corner atoms contribute 1/8 of an atom, face-centered atoms contribute 1/2, while body-centered atoms contribute fully (1 atom).
What is the contribution of a corner atom in a unit cell?
-A corner atom is shared equally by eight unit cells. As a result, each corner atom contributes only 1/8 of an atom to a particular unit cell.
How is a face-centered atom shared among unit cells?
-A face-centered atom is shared by two adjacent unit cells. Therefore, each face-centered atom contributes 1/2 of an atom to each unit cell.
What is the contribution of a body-centered atom in a unit cell?
-A body-centered atom is not shared by any other unit cell, so it contributes fully, or 1 atom, to the unit cell.
How is an edge-centered atom shared among unit cells?
-An edge-centered atom is shared by four adjacent unit cells. It contributes 1/4 of an atom to each unit cell.
How many atoms are there in a simple cubic unit cell?
-In a simple cubic unit cell, there are eight corner atoms, and each corner atom contributes 1/8 of an atom. Therefore, the total number of atoms in the unit cell is 1.
How many atoms are there in a body-centered cubic unit cell?
-A body-centered cubic unit cell contains 2 atoms. There are eight corner atoms contributing 1 atom (8 × 1/8 = 1), and one body-centered atom contributing 1 atom.
How many atoms are in a face-centered cubic unit cell?
-A face-centered cubic unit cell contains 4 atoms. There are eight corner atoms contributing 1 atom (8 × 1/8 = 1), and six face-centered atoms contributing 3 atoms (6 × 1/2 = 3).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
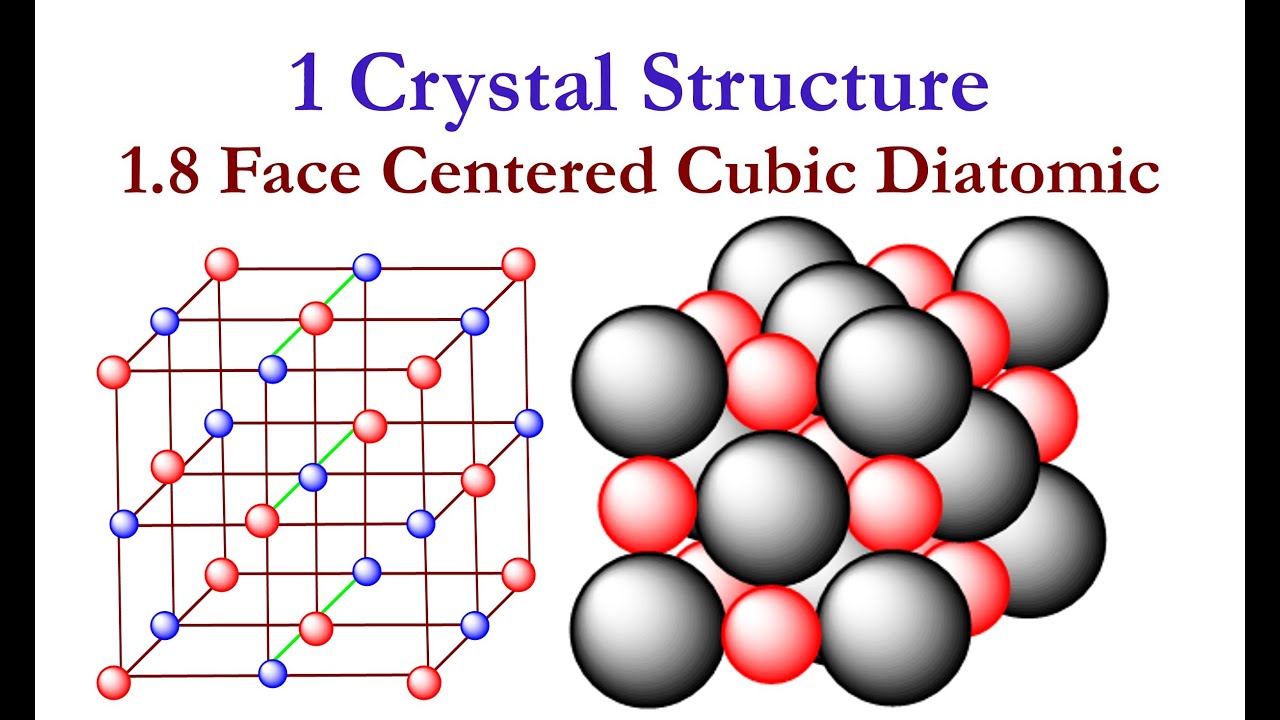
1 Crystal Structure: 1.8 Structure of NaCl #SodiumChlorideStructure #NaCl #CrystalStructure
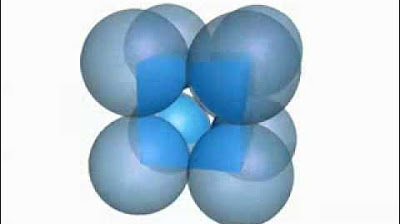
The primitive, body-centred and face-centred cubic unit cells

Lecture 3 Part 1 - Crystal Structure - 2 (Unit Cell, Lattice, Crystal)

noc19-cy16 Lecture 06-Solid state Chemistry-Week 2 Lecture-1 Unit Cell

Mole to particle Calculations

Cálculo do Fator de Empacotamento CFC e CS - Exercícios Resolvidos Callister (07)
5.0 / 5 (0 votes)