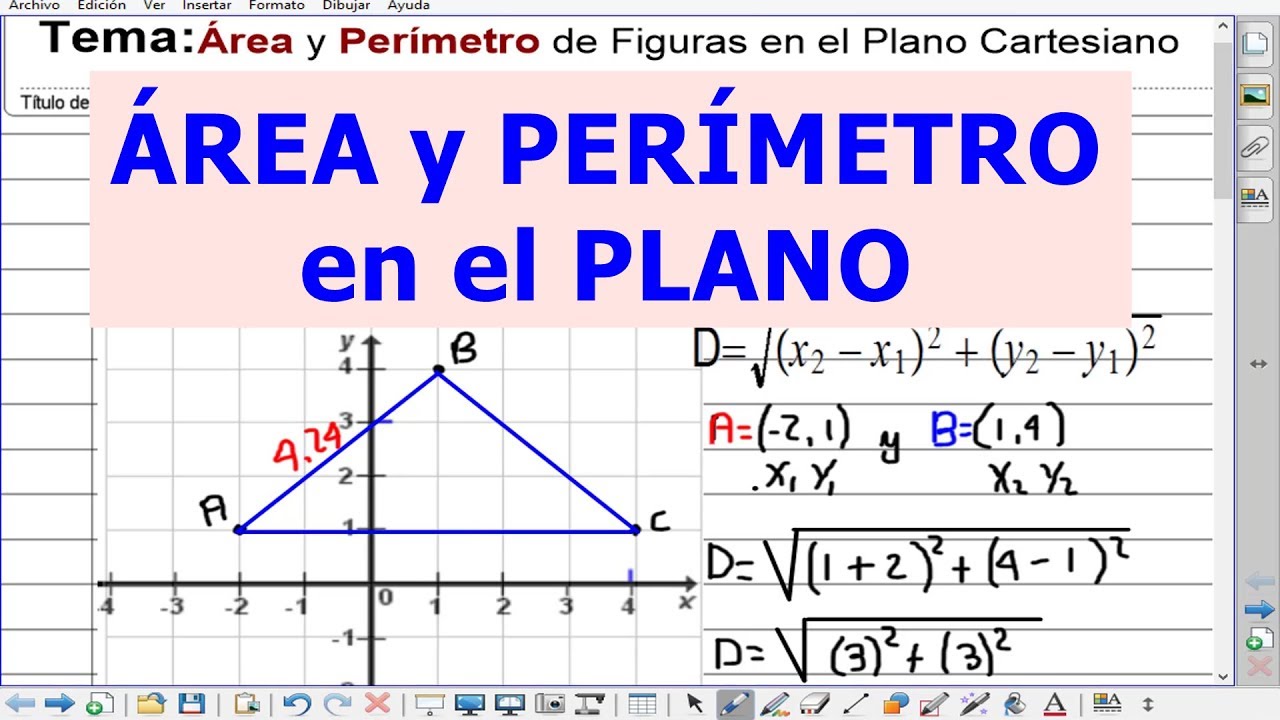
Demostración de la fórmula de Herón. Parte 1

KhanAcademyEspañol

12 Jan 201410:36

Summary

TLDREl guión de este video educativo se enfoca en demostrar la fórmula de Herón para calcular el área de un triángulo, utilizando solo las longitudes de sus lados. Comienza introduciendo una variable auxiliar 'x' para la distancia del vértice al pie de la altura, y luego aplica el teorema de Pitágoras en dos triángulos rectángulos. Tras resolver un sistema de ecuaciones, se encuentra la expresión para la altura 'H' en función de 'A', 'B' y 'C'. Finalmente, se simplifica para obtener una fórmula de área que solo depende de los lados del triángulo, comparando los resultados con un ejemplo concreto y confirmando la precisión de la fórmula obtenida.

Takeaways

📐 El script trata sobre cómo determinar el área de un triángulo dado sus lados A, B y C sin conocer la altura.
🚫 No se puede utilizar la fórmula clásica de área (base × altura / 2) debido a la falta de información sobre la altura.
📉 Se introduce una variable auxiliar 'x' para representar la distancia de un vértice al pie de la altura.
🔍 Se aplica el teorema de Pitágoras a dos triángulos rectángulos formados por la altura y los lados del triángulo.
🧩 Se establece un sistema de ecuaciones con dos variables (x y H) para encontrar la altura en términos de los lados del triángulo.
✂️ Se simplifica algebraicamente para despejar H y luego x, obteniendo una expresión para la altura H en función de A, B y C.
📈 Se utiliza la expresión de H para calcular el área del triángulo, derivando una fórmula que depende únicamente de A, B y C.
🔢 Se muestra que la fórmula obtenida es equivalente a la fórmula de Herón, aunque en una forma menos común.
📚 Se propone continuar con la simplificación algebraica en un próximo video para llegar a la fórmula de Herón más conocida.
📝 Se compara la nueva fórmula con un ejemplo del video anterior, utilizando los lados de 9, 11, 16 y 16, para verificar la consistencia y corrección de la fórmula.

Q & A

¿Qué fórmula clásica se menciona para encontrar el área de un triángulo?
-La fórmula clásica mencionada para encontrar el área de un triángulo es: Área = 1/2 * base * altura.
¿Por qué no se puede utilizar la fórmula clásica de área en este problema?
-No se puede utilizar la fórmula clásica porque, aunque se conoce la longitud de un lado como base, no se tiene información sobre la altura perpendicular a esta base.
¿Qué fórmula se propone utilizar en lugar de la fórmula clásica para calcular el área del triángulo?
-Se propone utilizar la fórmula de Herón para calcular el área del triángulo, dado que se conocen las longitudes de los lados A, B y C.
¿Qué es el teorema de Pitágoras y cómo se relaciona con el problema?
-El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. Se utiliza en el problema para relacionar la altura con las longitudes de los lados del triángulo.
¿Qué variable auxiliar se introduce para simplificar el problema?
-Se introduce la variable auxiliar 'x', que representa la distancia de un vértice al pie de la altura.
¿Cómo se relaciona la variable 'x' con la longitud de la base 'c' y la altura 'H'?
-La variable 'x' se relaciona con la base 'c' y la altura 'H' de la siguiente manera: si 'x' es la distancia del vértice al pie de la altura, entonces la longitud desde el pie de altura a ese vértice es 'c - x'.
¿Cómo se aplicó el teorema de Pitágoras para obtener una ecuación en términos de 'x' y 'H'?
-Se aplicó el teorema de Pitágoras a los dos triángulos rectángulos formados por la altura, obteniendo dos ecuaciones: x^2 + H^2 = A^2 y (c - x)^2 + H^2 = B^2.
¿Cómo se simplificó la ecuación para encontrar el valor de 'x' en términos de A, B y C?
-Se simplificó al eliminar H^2 de ambas ecuaciones, lo que llevó a una expresión que involucra A^2, B^2, C^2 y x, y luego se resolvió para encontrar x = (A^2 + C^2 - B^2) / (2C).
¿Cómo se encontró el valor de la altura 'H' en términos de A, B y C?
-Se sustituyó el valor de 'x' en la ecuación de H^2 = A^2 - x^2, lo que resultó en H = sqrt(A^2 - (A^2 + C^2 - B^2)^2 / (4C^2)).
¿Cómo se relaciona el área del triángulo con la fórmula de Herón y la altura 'H' encontrada?
-El área del triángulo se relaciona con la fórmula de Herón y la altura 'H' mediante la expresión: Área = 1/2 * base * H, donde 'base' es el lado C y 'H' es la altura perpendicular a este lado.
¿Cómo se verificó que la fórmula obtenida da el mismo resultado que la fórmula de Herón para un triángulo con lados 9, 11 y 16?
-Se sustituyeron los valores de los lados en la fórmula obtenida y se calculó el área, resultando en 47.62375, el cual es igual al área obtenido con la fórmula de Herón, lo que confirma la validez de la fórmula.

Outlines

00:00

📐 Demostración de la fórmula de Herón a través del teorema de Pitágoras

El primer párrafo introduce el problema de calcular el área de un triángulo dado sus lados A, B y C. Se menciona que la fórmula clásica de área (base por altura) no se puede aplicar debido a la falta de información sobre la altura. En su lugar, se sugiere la utilización de la fórmula de Herón, que se demostrará a través del uso del teorema de Pitágoras y simplificaciones algebraicas. Se introduce una variable auxiliar 'x' para representar la distancia de un vértice al pie de la altura y se establecen dos ecuaciones utilizando el teorema de Pitágoras en los triángulos rectángulos formados. La sección concluye con la resolución de un sistema de ecuaciones para encontrar la altura 'H' en función de los lados del triángulo.

05:01

🔍 Determinación de la altura y el área del triángulo

Este párrafo sigue el proceso de demostración de la fórmula de Herón. Se despeja la ecuación para encontrar la altura 'H' en términos de 'x' y los lados del triángulo. Luego, se sustituye el valor de 'x' y se resuelve para obtener 'H'. Con la altura obtenida, se procede a calcular el área del triángulo utilizando la fórmula 1/2 * base * altura. Se simplifica la expresión algebraicamente para obtener una fórmula de área que depende únicamente de los lados del triángulo (A, B y C). Se menciona que esta fórmula es equivalente a la de Herón, aunque tiene una apariencia diferente. Finalmente, se prueba la fórmula con un ejemplo de triángulo con lados de 9, 11, 16 y 16, obteniendo el mismo resultado de área que en un video anterior (18√7).

10:02

🎯 Validación de la fórmula de área y预告 del siguiente video

El tercer párrafo comienza con la confirmación de que la fórmula de área obtenida es correcta, ya que da el mismo resultado que el de un video anterior para un triángulo específico. Se recalca la importancia de esta fórmula, ya que permite calcular el área de un triángulo solo con la información de sus lados. El video parece estar en proceso de simplificar aún más la expresión algebraica para una fórmula más fácil de memorizar. El párrafo termina con una anticipación al siguiente video, donde se promete continuar con la simplificación y demostración de la fórmula de Herón.

Mindmap

Keywords

💡Triángulo

El triángulo es la figura geométrica principal del video, compuesta por tres lados y tres ángulos. Es fundamental para entender el tema central, ya que el objetivo es determinar el área de un triángulo dado las longitudes de sus lados. En el guion, el triángulo es descrito con lados A, B y C, y se utiliza para demostrar la fórmula de Herón.

💡Área

La área es una medida de la extensión de un triángulo en el plano. En el video, la fórmula clásica para calcular el área de un triángulo (base por altura dividido entre 2) no puede ser aplicada directamente debido a la falta de información sobre la altura. La búsqueda de una fórmula alternativa para calcular el área da inicio a la discusión del video.

💡Teorema de Pitágoras

El teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. En el script, se utiliza este teorema para resolver dos ecuaciones que involucran la distancia x desde un vértice hasta el pie de la altura y la altura H del triángulo.

💡Fórmula de Herón

La fórmula de Herón es una herramienta matemática que permite calcular el área de un triángulo si se conocen las longitudes de sus tres lados. El video trata demostrar por qué esta fórmula siempre es verdadera, utilizando el teorema de Pitágoras y simplificaciones algebraicas.

💡Altura

La altura (H) es la línea perpendicular desde un vértice del triángulo hasta la base opuesta. Aunque no se conoce inicialmente, se busca relacionarla con los lados del triángulo para aplicar el teorema de Pitágoras y eventualmente encontrar una fórmula para el área.

💡Variable auxiliar

La variable auxiliar, en este caso 'x', es una técnica común en geometría para introducir una nueva variable que ayude a resolver un problema. En el script, 'x' representa la distancia de un vértice al pie de la altura, lo que simplifica las ecuaciones y lleva a la fórmula de Herón.

💡Sistema de ecuaciones

Un sistema de ecuaciones es una colección de ecuaciones que se resuelve juntas para encontrar los valores de las variables involucradas. En el video, se presenta un sistema de ecuaciones con 'x' y 'H' como variables, que se resuelve para encontrar la altura del triángulo.

💡Simplificación algebraica

La simplificación algebraica es el proceso de reducir una expresión matemática a su forma más simple. En el guion, se realizan varios pasos de simplificación para llegar a una expresión de área que solo involucre los lados del triángulo, lo que es crucial para demostrar la fórmula de Herón.

💡Raíz cuadrada

La raíz cuadrada es una operación matemática que busca el valor que, al elevarse al cuadrado, da un número dado. En el script, se utiliza para calcular la altura del triángulo y, posteriormente, para encontrar la expresión de la fórmula de Herón.

💡Ecuación

Una ecuación es una afirmación matemática que equilibra dos expresiones, indicando que son iguales. En el video, las ecuaciones surgen del teorema de Pitágoras y son esenciales para relacionar las variables 'x' y 'H' con los lados del triángulo.

Highlights

Se presenta un método para determinar el área de un triángulo dado sus lados A, B y C sin utilizar la fórmula clásica de base por altura.

Se introduce la fórmula de Herón como una alternativa para calcular el área del triángulo.

Se propone demostrar la fórmula de Herón utilizando el teorema de Pitágoras y simplificaciones algebraicas.

Se introduce una variable auxiliar 'x' para la distancia del vértice al pie de la altura.

Se aplica el teorema de Pitágoras a dos triángulos rectángulos para establecer un sistema de ecuaciones.

Se resuelve el sistema de ecuaciones para encontrar la expresión de 'H' en términos de A, B y C.

Se simplifica la expresión de 'H' y se obtiene una fórmula para calcular la altura del triángulo.

Se utiliza la fórmula de la altura para determinar el área del triángulo en función de sus lados.

Se muestra que la fórmula obtenida es equivalente a la fórmula de Herón, aunque en una forma menos conocida.

Se realiza una comparación con un ejemplo de un triángulo con lados de 9, 11, 16 y 16 para validar la fórmula.

Se calcula el área del triángulo del ejemplo utilizando la nueva fórmula y se obtiene un resultado coherente con el anterior.

Se sugiere que la fórmula obtenida puede ser memorizada y utilizada para calcular áreas de triángulos sin necesidad de la altura.

Se destaca la importancia de las simplificaciones algebraicas en el proceso de demostración de la fórmula de Herón.

Se planifica para el próximo video la simplificación de la expresión algebraica para que coincida con la fórmula de Herón más común.

Se enfatiza la consistencia y la precisión en el proceso matemático como una buena indicación de que se está siguiendo el camino correcto.

Se concluye que la demostración de la fórmula de Herón es un buen ejemplo de cómo se pueden derivar fórmulas matemáticas a partir de teoremas clásicos.