Circuncentro de un triángulo
Summary
TLDREl video ofrece una explicación detallada sobre la construcción y propiedades de las medianas en un triángulo. Comienza trazando una segmento de línea y su respectiva mediana perpendicular, demostrando que cualquier punto en la mediana equidista los extremos del segmento. Luego, aplica este concepto a un triángulo, donde las tres medianas se intersectan en un punto conocido como el centro de la circunferencia circunscrita, también llamado el círculo un centro. El video concluye con la introducción de la circunferencia circunscrita, una circunferencia que pasa por los tres vértices del triángulo, y su relación con el centro de la circunferencia circunscrita.
Takeaways
- 📏 El video comienza explicando cómo trazar una mediana 'l' de un segmento 'ave', que es una recta perpendicular que pasa por el punto medio del segmento.
- 📐 Se denomina 'l' a la mediana y se busca probar que cualquier punto sobre 'l' equidista de 'a' y 'b', es decir, la distancia 'aa' es igual a la distancia 'ab'.
- 📍 Se utiliza el punto 'c' sobre la mediana 'l' para demostrar la equidistancia mediante la construcción de segmentos y la observación de triángulos del ángulo recto.
- 🔍 Se establece la congruencia de dos triángulos rectángulos, 'AMC' y 'BMC', por el criterio de lado-ángulo-lado, para concluir que 'AC' es congruente a 'BC'.
- 🔄 Se intenta probar la afirmación al revés: si un punto equidista de 'a' y 'b', entonces está sobre la mediana del segmento 'ab', utilizando la construcción de alturas y triángulos congruentes.
- 📐 Se demuestra que si un punto 'c' está sobre la mediana 'l', entonces 'b' es igual a 'm', lo que confirma que 'm' es una mediana.
- 🤔 Se plantea la idea de que el argumento es aplicable independientemente de la ubicación del punto 'c' sobre la mediana.
- 🔶 Se utiliza el conocimiento recién descubierto sobre puntos equidistantes y medianas para trabajar con triángulos, iniciando con la construcción de las tres medianas en un triángulo 'ABC'.
- 🔄 Se observa que las tres medianas de un triángulo se intersectan en un solo punto, denominado 'O', el cual cumple ser equidistante de los vértices 'A', 'B' y 'C'.
- 🌐 Se introduce el concepto del 'círculo circumscribedo' o circunferencia circunscrita, que es una circunferencia que pasa por los tres vértices de un triángulo y tiene como centro el punto 'O', el círculo un centro del triángulo.
Q & A
¿Qué es un segmento de ave y cómo se define?
-Un segmento de ave es una parte de un triángulo que une a dos vértices. Se define como el segmento de línea recta que une dos puntos (vértices) de un triángulo.
¿Cómo se traza la mediatriz de un segmento de ave y cuál es su importancia?
-Para trazar la mediatriz, se dibuja una recta perpendicular al segmento que pase por su punto medio. La mediatriz es importante porque equidista a los extremos del segmento, cumpliendo con la propiedad de ser un segmento perpendicular y de punto medio.
¿Qué es un ángulo recto y cómo se identifica en el script?
-Un ánglo recto es un ángulo de 90 grados. En el script, se identifican ángulos rectos al mencionar que la mediatriz es perpendicular al segmento de ave, lo que implica ángulos rectos en las intersecciones.
¿Cómo se demuestra que cualquier punto sobre la mediatriz equidista los puntos a y b?
-Se toma un punto c sobre la mediatriz y se trazan los segmentos ac y bc. Se demuestra que los triángulos amc y bmc son congruentes por el criterio lado-ángulo-lado, lo que implica que ac es igual a bc, probando así que el punto c equidista a y b.
¿Qué es un triángulo congruente y cómo se demuestra que dos triángulos son congruentes en el script?
-Un triángulo congruente es uno que tiene las mismas medidas de lado y ángulos que otro triángulo. En el script, se demuestra la congruencia de los triángulos amc y bmc utilizando el criterio lado-ángulo-lado, donde los lados y ángulos correspondientes son iguales.
¿Qué es el punto o y cómo se relaciona con las mediatrices de un triángulo?
-El punto o es el punto de intersección de las tres mediatrices de un triángulo. Se relaciona con las mediatrices porque es equidistante a los tres vértices del triángulo y está sobre cada una de las mediatrices.
¿Qué se llama al círculo que tiene como centro al punto o y pasa por los tres vértices del triángulo?
-El círculo que tiene como centro al punto o y pasa por los tres vértices del triángulo se llama círculo circunscrito o circunferencia circunscrita.
¿Cómo se demuestra que el punto o está sobre la mediatriz de bc?
-Se traza la altura de c a la mediatriz de ave, se llama a este punto m y se demuestra que cm es igual a bm, lo que implica que el punto m es la mediatriz. Al demostrar que bm es igual a mc, se concluye que el punto o está sobre la mediatriz de bc.
¿Qué propiedades cumple el punto o y cómo se deduce que es el centro del círculo circunscrito?
-El punto o cumple la propiedad de ser equidistante a los tres vértices del triángulo y está sobre las tres mediatrices. Se deduce que es el centro del círculo circunscrito porque toda circunferencia con centro en o y radio oa, ob o oc, pasa por los vértices del triángulo.
¿Cuál es la relación entre el círculo circunscrito y el punto o en el triángulo abc?
-El círculo circunscrito es una circunferencia que tiene como centro al punto o y radio igual a la distancia de o a cualquier vértice del triángulo abc, y pasa por todos los vértices del triángulo.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

EL CONCRETO Y SU DOSIFICACIÓN | Paso a paso para principiantes

MICRO EMPRESAS, PEQUEÑAS EMPRESAS, MEDIANAS EMPRESAS Y GRANDES EMPRESAS EN EL PERU
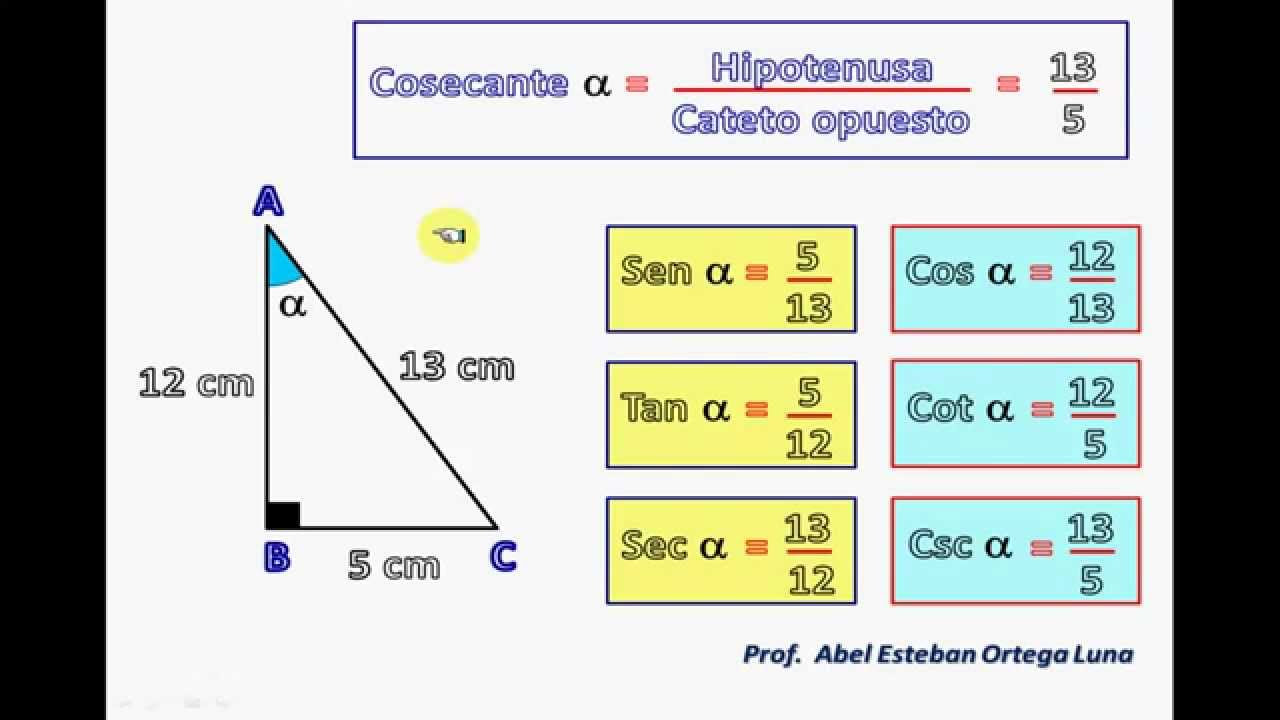
RAZONES TRIGONOMÉTRICAS EN UN TRIÁNGULO RECTÁNGULO

CÁLCULO DE DENSIDADES DE MATERIALES
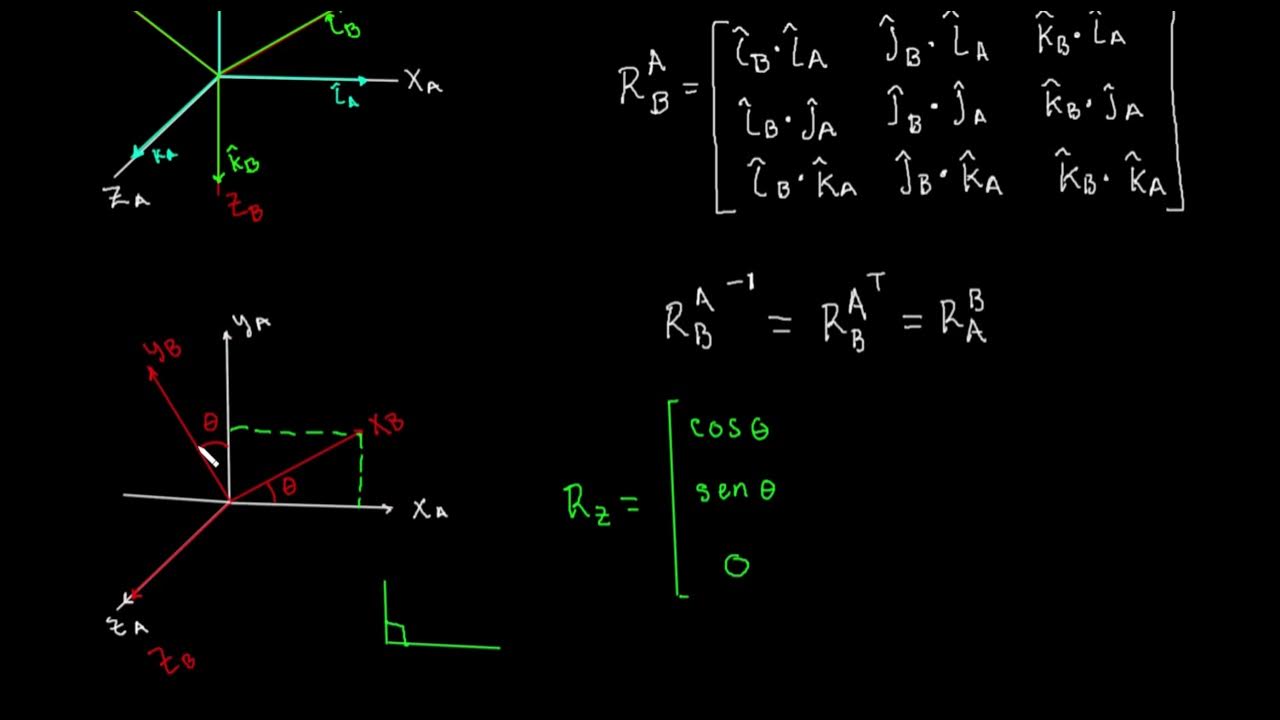
Matrices de rotación en 3D de x, y, z

número atomico, número de masa e isotopos
5.0 / 5 (0 votes)
