Konsep Dasar Batang Tekan & Euler Buckling Load | Struktur Baja | Lightboard
Summary
TLDRThis video explores the concept of compressive axial forces in structural engineering, focusing on the analysis of compression members. It introduces key concepts such as critical buckling load and explains how factors like the material's modulus of elasticity, the cross-sectional area, and the length of the column impact its ability to resist buckling. Using real-world examples like bridges and steel frameworks, the video highlights the differences between tension and compression members, delving into the calculations and implications of critical buckling load and its effects on structural stability.
Takeaways
- 😀 The speaker introduces two young daughters who often compete but also seek each other out when separated, highlighting sibling dynamics in a playful analogy to structural elements.
- 😀 The main focus of the video is on analyzing compressive members (batang tekan) in structural engineering, particularly in the context of bridges and buildings.
- 😀 The difference between tensile members (batang tarik) and compressive members (batang tekan) is discussed, with compressive members subject to potential buckling or flexural failure.
- 😀 Buckling in compressive members, also known as 'flexural failure,' occurs when the member bends under load, which doesn't happen in tensile members.
- 😀 The concept of 'critical buckling load' (P critical) is introduced, referring to the minimal force that causes a compressive member to buckle.
- 😀 The critical buckling load is influenced by several factors, including the length of the member (longer members are more prone to buckling), material elasticity (e.g., steel vs wood), and the shape of the cross-section.
- 😀 A mathematical formula for calculating P critical is presented, with a discussion of its components such as modulus of elasticity (E), the moment of inertia (I), and the length of the column (L).
- 😀 The speaker explains the relationship between a column's slenderness ratio (L/r), where more slender columns are more likely to buckle under smaller loads.
- 😀 The differences between elastic and inelastic buckling are explored. Elastic buckling refers to when a column returns to its original shape after unloading, whereas inelastic buckling results in permanent deformation.
- 😀 The video also touches on the use of LRFD (Load and Resistance Factor Design) and further calculations to account for critical buckling under different conditions, particularly for slender columns.
Q & A
What are the two main forces discussed in the video related to structural members?
-The two main forces discussed are tensile forces (batang tarik) and compressive forces (batang tekan). Tensile forces cause elongation, while compressive forces cause shortening or buckling in structural members.
How do compression members behave under axial loads according to the video?
-Compression members experience axial compressive forces, which can lead to buckling if the forces exceed the critical buckling force, depending on factors like the member's length, material properties, and cross-sectional shape.
What is the critical buckling force and why is it important?
-The critical buckling force is the minimal axial load that causes a compression member to start buckling. It's important because it helps determine the maximum load a column can carry before failure due to instability.
What does the modulus of elasticity (E) represent in the context of compression members?
-The modulus of elasticity (E) represents the material's stiffness, indicating how much it resists deformation under stress. A higher E value means the material is stiffer and more resistant to buckling.
What is the difference between 'elastic buckling' and 'inelastic buckling'?
-Elastic buckling occurs when the compression member deforms temporarily under load but returns to its original shape once the load is removed. Inelastic buckling involves permanent deformation, and the member does not return to its original shape after unloading.
How does the length of a compression member (L) influence its susceptibility to buckling?
-The longer the compression member, the easier it is for it to buckle. This is because the critical buckling force decreases as the length increases, making longer members more prone to buckling.
What role does the cross-sectional area (A) play in determining the critical buckling force?
-The cross-sectional area directly affects the critical buckling force; a larger cross-sectional area results in a higher critical buckling force, making the member less prone to buckling.
How does the moment of inertia (I) affect the buckling behavior of a member?
-The moment of inertia (I) relates to the shape and size of the cross-section. A higher moment of inertia reduces the susceptibility to buckling, as it helps distribute the load more effectively, making the member stiffer.
What does the term 'slenderness ratio' mean in the context of structural columns?
-The slenderness ratio is the ratio of the effective length of a column to its radius of gyration. A higher slenderness ratio indicates a more slender and potentially less stable column, which is more susceptible to buckling.
What factors affect the critical buckling force according to the video?
-The critical buckling force is influenced by several factors: the column's length, the material's modulus of elasticity, and the cross-sectional shape and area (which determine the moment of inertia and radius of gyration).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

SK04A Struktur Kayu Contoh soal Truss Part 1
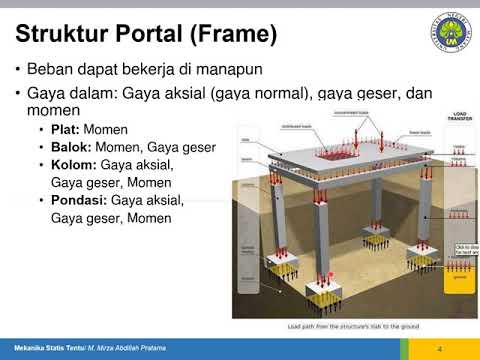
Mekanika Statis Tentu: Klasifikasi Struktur Bangunan

Structural Theory 1 Chapter 1 Structural Elements & Types of Structure Part 1 (with Subtitles)

PENGERTIAN DAN JENIS-JENIS GAYA DALAM PADA STRUKTUR - MUDAH

Structural Theory 1 Chapter 1 Part III (with Subtitles)

S-10 Pengenalan Truss
5.0 / 5 (0 votes)