Boolean Algebra for PLCs Explained | Basics
Summary
TLDRThis video introduces Boolean algebra concepts essential for PLC ladder programming. It covers basic logical operations such as NOT, AND, and OR, with practical examples on how these operations are used in PLCs. The video also explores derived functions like XOR and XNOR, and discusses methods for simplifying Boolean expressions using standard forms and Karnaugh maps. A real-world example of controlling a drilling system is used to demonstrate how to derive and simplify Boolean expressions for PLC implementation. The video concludes with tips for implementing simplified expressions in PLC systems for efficient automation.
Takeaways
- 😀 Boolean algebra is essential for programming a PLC, especially for ladder logic programming.
- 😀 The 'NOT' or negation operation is the simplest logical operation, which inverts the input value (0 becomes 1 and vice versa).
- 😀 The 'AND' operation requires both inputs to be high (1) for the output to be high, similar to two switches in series.
- 😀 The 'OR' operation gives a high output if at least one of the inputs is high, like two switches in parallel.
- 😀 Logical operations can be represented with truth tables, ISO symbols, and electrical schematics.
- 😀 The 'Exclusive OR' (XOR) operation gives a high output if only one of the inputs is high, but not both.
- 😀 The 'Equivalence' (XNOR) operation outputs high when both inputs are the same (either both 0 or both 1).
- 😀 'NAND' and 'NOR' operations are the negations of 'AND' and 'OR' respectively.
- 😀 To implement Boolean expressions practically, they need to be simplified using Boolean algebra before creating the corresponding circuits.
- 😀 Two methods for deriving simplified Boolean expressions from truth tables are the Disjunctive Standard Form (Sum of Products) and Conjunctive Standard Form (Product of Sums).
- 😀 Karnaugh Maps (K-Maps) can be used to simplify Boolean expressions by grouping cells with 1s and deriving the simplest possible expression.
Q & A
What is the simplest logical operation discussed in the video?
-The simplest logical operation discussed in the video is the NOT (negation) operation. It is a single-input operation that flips the input: a zero becomes one, and a one becomes zero.
How is the NOT operation represented in electrical circuits?
-In electrical circuits, the NOT operation can be implemented using a normally closed switch. When the switch is open (input is high), the output is off. When the switch is closed (input is low), the output is on.
What is the key difference between the AND and OR logical operations?
-The AND operation requires both inputs to be high (1) for the output to be high, while the OR operation only requires one input to be high (1) for the output to be high.
What is the significance of the truth table in Boolean algebra?
-A truth table lists all possible combinations of input values and their corresponding output for a given logical operation. It helps in understanding how logical functions behave and in deriving Boolean expressions.
Can you explain the concept of 'Exclusive OR' (XOR)?
-Exclusive OR (XOR) is a logical operation that outputs high (1) only if exactly one of the two inputs is high. If both inputs are either high or both low, the output is low (0).
What is a Karnaugh map (K-map), and how is it used in Boolean simplification?
-A Karnaugh map (K-map) is a graphical representation used to simplify Boolean expressions. It organizes the truth table into a grid and allows the identification of groups of ones, which are then used to derive simplified Boolean expressions.
How does the disjunctive standard form (Sum of Products) method work in Boolean expression derivation?
-In the disjunctive standard form, the Boolean expression is derived by taking the disjunction (OR) of conjunctions (AND) of input variables that correspond to output 1 in the truth table. This method ensures the expression is simplified to handle specific conditions.
What are the benefits of simplifying a Boolean expression before implementing it in hardware?
-Simplifying a Boolean expression reduces the number of logic gates required, leading to more efficient and cost-effective hardware implementations. It also reduces complexity, making the system easier to troubleshoot and maintain.
What does the 'Product of Sums' method in Boolean expression derivation involve?
-The 'Product of Sums' method involves writing down the disjunction (OR) of inputs that lead to output 0 and then taking the conjunction (AND) of these expressions. This method is particularly useful when the number of zeros in the truth table is greater than the number of ones.
How does the AND gate differ from the OR gate in terms of output conditions?
-An AND gate requires all its inputs to be high (1) for the output to be high (1). In contrast, an OR gate only requires one input to be high (1) for the output to be high (1), making the OR gate less restrictive in its output conditions.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Ladder Logic Diagrams for PLCs | Industrial Automation

DASAR PEMOGRAMAN PLC - SIMBOL - SIMBOL DASAR PLC

Matdis 19: Aljabar Boolean (Segmen 1: Apa itu Aljabar Boolean)
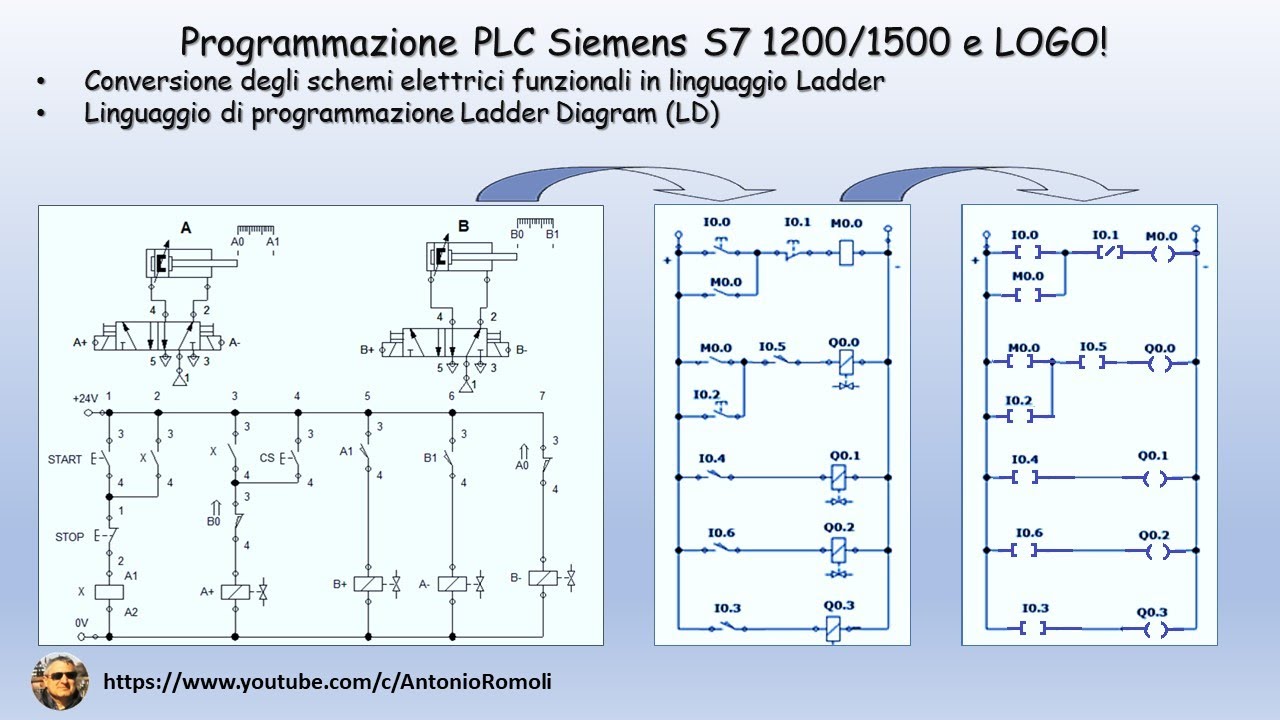
PLC: convertire lo schema elettrico funzionale in linguaggio di programmazione Ladder (Video 1.1)

Example PLC: EATON EASY Intelligent Relay (Full Lecture)

10 Math Concepts for Programmers
5.0 / 5 (0 votes)