Algoritma K-Means Klustering Data Mining | Seri Data Mining #5

Summary

In this video, the speaker delves into the concept of K-Means clustering within the field of data mining. The explanation covers the algorithm’s functionality, including the process of partitioning data into clusters based on similarity using distance metrics like Euclidean distance. The video also highlights practical applications in healthcare (COVID-19 mapping), geography (disease tracking), and business (customer segmentation). Emphasizing unsupervised learning, the video guides viewers through the iterative steps of K-Means clustering, from random initialization of centroids to reassigning data points and refining clusters, offering a comprehensive and insightful look into this powerful algorithm.

Takeaways

• 😀 Clustering is an unsupervised learning method in data mining, where data is grouped into clusters without predefined labels or outputs.
• 😀 K-means clustering is one of the most popular clustering algorithms that uses distance metrics to group data into clusters.
• 😀 Among distance metrics, the Euclidean distance is found to be the best for K-means clustering, as shown by studies like those from Shinhwa (2014), Om (2019), and Sing (2013).
• 😀 Clustering can be applied to real-world problems, such as mapping COVID-19 cases in a region to help governments plan interventions.
• 😀 Geographic Information Systems (GIS) can be integrated with clustering algorithms to analyze diseases like dengue fever (DBD) in areas like Surabaya.
• 😀 Businesses can also use clustering for targeted promotions by identifying loyal customers and avoiding wasteful advertising to disinterested customers.
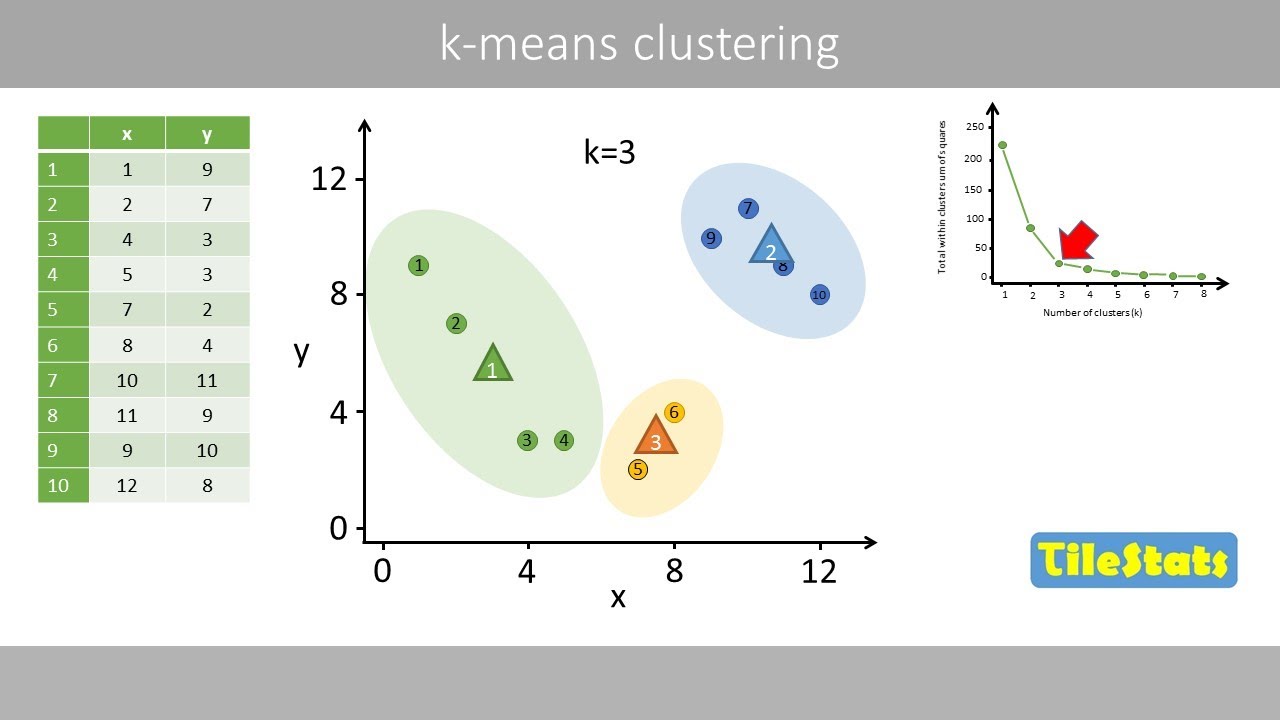
• 😀 In K-means clustering, the algorithm iterates by adjusting centroids based on the proximity of data points to those centroids until stabilization occurs.
• 😀 Clustering differs from classification because there are no labels or target attributes; instead, the algorithm groups similar data points together.
• 😀 K-means clustering uses random initialization of centroids, and in each iteration, it assigns data points to the nearest centroid and recalculates new centroids.
• 😀 The final clusters are formed when no data points change groups between iterations, indicating convergence of the algorithm.

Q & A

What is the main topic discussed in the video?

The video primarily focuses on K-means clustering, an algorithm used in data mining to group similar data points without predefined labels. It also compares different distance metrics like Euclidean, Manhattan, and Minkowski for evaluating clustering effectiveness.

How does K-means clustering differ from supervised learning algorithms?

K-means clustering is an unsupervised learning algorithm, meaning it does not require labeled data or predefined output categories. Unlike supervised learning, which uses known labels to train a model, clustering groups data based on inherent similarities, without predefined outcomes.

What are the primary steps involved in the K-means clustering process?

The K-means clustering process involves three main steps: 1) Select initial centroids randomly. 2) Assign data points to the nearest centroid based on a chosen distance metric. 3) Recalculate centroids as the average of the assigned points and repeat the process until the centroids no longer change.

What is the role of distance metrics in K-means clustering?

Distance metrics determine how the algorithm measures the 'closeness' between data points and centroids. Common distance metrics used in K-means clustering include Euclidean distance (straight-line distance), Manhattan distance (grid-based path distance), and Minkowski distance (a generalized version of the other two).

Can you explain the difference between Euclidean and Manhattan distance?

Euclidean distance is the straight-line distance between two points, calculated using the Pythagorean theorem. In contrast, Manhattan distance measures the sum of the absolute differences between the coordinates of two points, effectively calculating the distance by only moving along grid lines (like city blocks).

How is K-means clustering applied in healthcare data analysis?

In healthcare, K-means clustering can be used for tasks such as grouping patients based on symptoms, predicting disease outbreaks, or identifying high-risk areas for certain conditions, as seen in the example of COVID-19 patient clustering in Situbondo.

What practical applications of K-means clustering are discussed in the video?

The video discusses several practical applications of K-means clustering, including COVID-19 patient clustering in Situbondo, disease mapping for DBD in Surabaya, and customer segmentation in businesses for targeted marketing.

What is the significance of the centroid in the K-means clustering algorithm?

The centroid in K-means clustering represents the center of a cluster. It is calculated as the mean of all data points assigned to that cluster. The algorithm iteratively updates centroids based on the mean of assigned points, and the process continues until the centroids stabilize.

What happens if the centroids do not change during an iteration in K-means clustering?

If the centroids do not change during an iteration, the algorithm has converged, meaning it has successfully grouped the data into clusters. At this point, the clustering process is complete, and no further updates to centroids or data point assignments are necessary.

How does K-means clustering benefit businesses in terms of customer segmentation?

For businesses, K-means clustering can be used to segment customers into groups based on behavior, such as loyalty or spending patterns. This allows companies to target specific customer groups with tailored marketing campaigns, thereby improving efficiency and increasing sales.