Partial derivatives, introduction
Summary
TLDRThis video explains the concept of partial derivatives, focusing on how they relate to ordinary derivatives. It starts by reviewing the basics of single-variable derivatives and introduces multi-variable functions, using an example with two variables (X and Y). The video emphasizes that partial derivatives isolate changes in one variable while treating others as constants, drawing parallels to the process of ordinary differentiation. It also covers the notation for partial derivatives and how to compute them, both at specific points and as general formulas, providing a foundational understanding of this essential concept in multivariable calculus.
Takeaways
- 😀 A multi-variable function like F(X, Y) can be differentiated using partial derivatives, where each derivative focuses on one variable while treating others as constants.
- 😀 Ordinary derivatives, like df/dx, represent how a tiny change in the input (X) influences the output, typically visualized on a graph as the slope of a curve.
- 😀 In partial derivatives, the concept is similar, but we evaluate how small changes in one input variable (X or Y) affect the output while keeping the other variable constant.
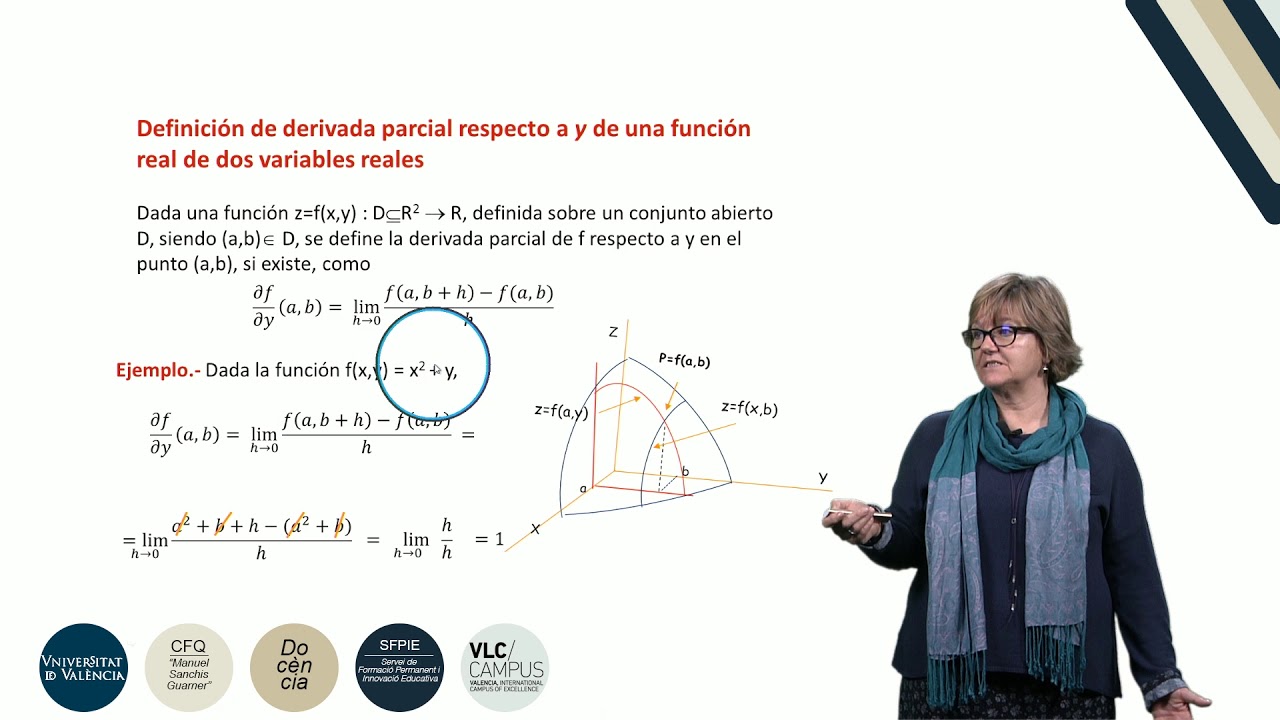
- 😀 For a function like F(X, Y) = X²Y + sin(Y), partial derivatives are computed by treating one variable as a constant while differentiating with respect to the other.
- 😀 The Leibniz notation for ordinary derivatives (df/dx) represents a small change in the function's output (df) relative to a small change in input (dx). This is analogous to slope in single-variable calculus.
- 😀 The graphical interpretation of a partial derivative involves a number line for the output, where changes in the X or Y direction affect the value of the function at a given point.
- 😀 The notation for partial derivatives includes a curly 'd' (∂), which distinguishes them from ordinary derivatives and emphasizes that they involve multi-variable functions.
- 😀 When computing partial derivatives, you take the derivative of the function with respect to one variable while treating the other variables as constants, leading to expressions that are simpler than full multi-variable derivatives.
- 😀 The result of a partial derivative gives you how the function changes with respect to a single direction (X or Y) at a specific point.
- 😀 Partial derivatives are often used in more general forms, such as ∂F/∂X, where you differentiate the function with respect to X while treating Y as a constant. This process can be repeated for other variables, like Y.
- 😀 Understanding partial derivatives is crucial for higher dimensions and multi-variable calculus, where the concept of graphs becomes less practical, and thinking in terms of directional changes in inputs becomes essential.
Q & A
What is the key difference between ordinary derivatives and partial derivatives?
-The key difference is that ordinary derivatives measure how a function changes with respect to a single variable, while partial derivatives measure how a multi-variable function changes with respect to one variable, holding all other variables constant.
How does the notation for partial derivatives differ from ordinary derivatives?
-In partial derivatives, the symbol '∂' (a D with a curl at the top) is used instead of 'd' to emphasize that the derivative is taken with respect to one variable while treating others as constants. For example, partial derivative with respect to x is written as ∂f/∂x.
Why are partial derivatives called 'partial' derivatives?
-They are called 'partial' because they only consider the effect of changing one variable while keeping others constant. This gives only a partial view of how the function changes with respect to all variables.
How do you compute a partial derivative of a function with respect to one variable?
-To compute a partial derivative, you treat all variables except the one you're differentiating with respect to as constants, then take the derivative as you would for a single-variable function.
What is the process for taking the partial derivative of the function f(x, y) = x²y + sin(y) with respect to x?
-To take the partial derivative of f(x, y) = x²y + sin(y) with respect to x, treat y as a constant. Differentiate x²y with respect to x, giving 2xy, and note that the derivative of sin(y) with respect to x is 0 because y is treated as constant.
What is the result when you compute the partial derivative of f(x, y) = x²y + sin(y) with respect to y at the point (1, 2)?
-When you compute the partial derivative of f(x, y) = x²y + sin(y) with respect to y at the point (1, 2), the result is 1 + cos(2), since the derivative of x²y with respect to y is x², and the derivative of sin(y) with respect to y is cos(y).
Why does the partial derivative with respect to y treat x as a constant?
-The partial derivative with respect to y treats x as a constant because we are only concerned with how the function changes as y changes, not x. This isolates the effect of y on the function.
How does visualizing a multi-variable function differ from visualizing a single-variable function?
-For a single-variable function, you can graph it as a curve, showing the relationship between the input and output. For a multi-variable function, the input space is more complex (such as the xy-plane), and the output is just a number, making it harder to visualize directly. Partial derivatives help quantify how changes in each variable influence the output.
Why is it important to understand the concept of partial derivatives in multi-variable calculus?
-Understanding partial derivatives is crucial because they allow us to analyze the behavior of functions that depend on multiple variables, such as in optimization problems, physics, and engineering, where multiple factors can influence a result simultaneously.
What does the term 'nudge' refer to in the context of derivatives?
-The term 'nudge' refers to a small change in the input variable (e.g., dx or dy) used to observe how the output of the function changes. The derivative measures the rate of change of the output relative to this small change in the input.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Derivadas parciales. Interpretación geométrica

Persamaan Diferensial Parsial (Pengertian, Definisi, dan Klasifikasi)

Partial Derivatives (Part 1)

Introduction to Differential Equations (Differential Equations 2)

Fisika Komputasi - Metode Finite Difference 05 Sifat Diferensial dan Persamaan Diferensial

Pengantar Persamaan Diferensial
5.0 / 5 (0 votes)