Support Vector Machine: Pengertian dan Cara Kerja
Summary
TLDRThis video explains Support Vector Machines (SVM), a supervised machine learning algorithm used for classification tasks. The speaker introduces the concept of SVM as a linear classifier, focusing on how it separates data into two classes using a hyperplane. For non-linear data, SVM applies a kernel trick to map data into higher dimensions for separation. Key concepts include hyperplanes, margins, and support vectors, with the speaker explaining how maximizing the margin between classes leads to better classification. The video also covers the mathematics behind SVM, showing how support vectors determine the optimal hyperplane.
Takeaways
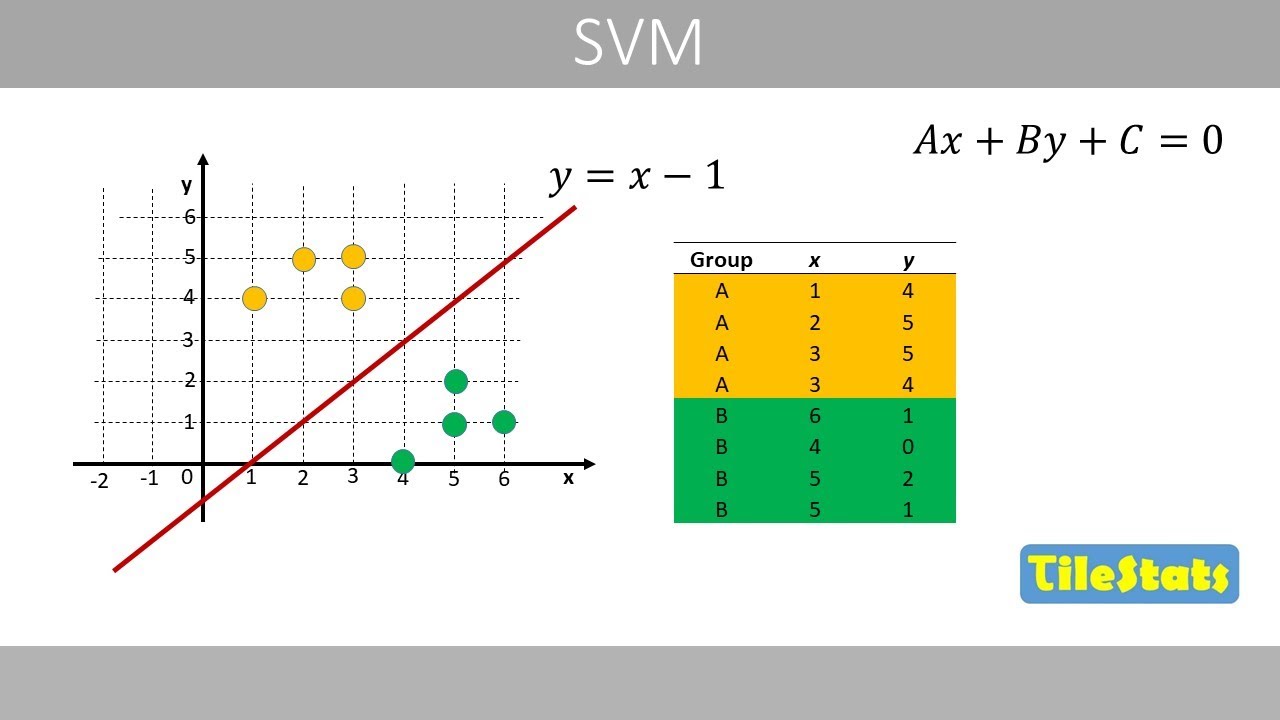
- 😀 Support Vector Machine (SVM) is a supervised machine learning method used for classification tasks, aiming to separate two classes of data.
- 😀 SVM works by finding a hyperplane that best separates the data in n-dimensional space. In 2D, this hyperplane is represented by a line.
- 😀 The primary principle behind SVM is to maximize the margin, which is the distance between the hyperplane and the closest data points from both classes, known as support vectors.
- 😀 Linear SVM can only classify linearly separable data, where a straight line (or hyperplane in higher dimensions) can perfectly separate the two classes.
- 😀 Nonlinear SVM addresses cases where the data is not linearly separable by adding higher dimensions to the data, creating a more complex separating surface.
- 😀 The goal of SVM is to find the optimal hyperplane, the one that provides the maximum margin between the classes.
- 😀 Support vectors are the data points that lie closest to the hyperplane and are crucial for defining the margin and the hyperplane itself.
- 😀 If the support vectors are not selected correctly, the hyperplane may not effectively separate the classes, leading to poor classification.
- 😀 SVM can handle both linear and nonlinear classification problems, with nonlinear cases requiring transformations to higher dimensions to separate the classes.
- 😀 In a nonlinear SVM, an additional dimension (e.g., Z = X² + Y²) is used to map the data into a new space where a linear separator can be applied.
- 😀 The optimal hyperplane in nonlinear SVMs can be visualized by projecting the transformed data onto lower dimensions, where it appears as a simple boundary (e.g., a circle).
Q & A
What is the basic principle behind Support Vector Machine (SVM)?
-The basic principle of Support Vector Machine (SVM) is to find the optimal hyperplane that best separates two classes in a dataset. SVM aims to maximize the margin, which is the distance between the hyperplane and the closest data points, called support vectors.
What are support vectors in SVM?
-Support vectors are the data points that are closest to the hyperplane. These points are critical for determining the position of the hyperplane. Only the support vectors are used to define the optimal hyperplane, and the rest of the data points do not affect its position.
What is the difference between linear and non-linear SVM?
-Linear SVM works when the data can be separated by a straight line or hyperplane in its original space. Non-linear SVM is used when data cannot be separated by a straight line, and it transforms the data into a higher-dimensional space using kernel functions to find a separating hyperplane.
How does SVM handle non-linear data?
-SVM handles non-linear data by applying the kernel trick, which maps the data into a higher-dimensional space where a hyperplane can be found to separate the classes. This allows SVM to classify data that is not linearly separable in the original space.
What is a margin in SVM, and why is it important?
-A margin in SVM is the distance between the hyperplane and the closest data points from each class (support vectors). The goal is to maximize this margin because a larger margin typically results in better generalization, reducing the risk of overfitting.
What does the term 'hyperplane' refer to in SVM?
-In SVM, a hyperplane is a decision boundary that separates different classes in the feature space. In 2D, it is a line; in 3D, it is a plane. For higher-dimensional data, it becomes a hyperplane in n-dimensional space.
What role does the kernel function play in non-linear SVM?
-The kernel function in non-linear SVM allows for the transformation of data into a higher-dimensional space where a linear hyperplane can separate the classes. It enables SVM to efficiently handle non-linearly separable data without explicitly calculating the higher-dimensional space.
What is the optimal hyperplane in SVM?
-The optimal hyperplane in SVM is the one that maximizes the margin between the classes. It is determined by the support vectors, and its position ensures the best classification of the data points while maintaining the maximum possible margin.
Why are only the support vectors used in SVM?
-Support vectors are the critical points that lie closest to the hyperplane. They are the only data points that directly affect the positioning of the hyperplane. The other points are not as influential in determining the optimal hyperplane, making support vectors the key elements in the classification process.
How does SVM perform classification in higher-dimensional spaces?
-In higher-dimensional spaces, SVM finds a hyperplane that separates the data points into different classes, just as it does in lower dimensions. The complexity increases as the dimensionality increases, but the principle remains the same: SVM searches for the hyperplane that maximizes the margin between the classes.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Support Vector Machines (SVM) - the basics | simply explained

All Learning Algorithms Explained in 14 Minutes

Eps-03 Learning Methods
Gender and Age Detection using CNN and SVM classifier | DL Project.

K-Nearest Neighbors Classifier_Medhanita Dewi Renanti

What is Deep Belief Networks (DBN) in Machine Learning?
5.0 / 5 (0 votes)