SISTEMI LINEARI metodo di CRAMER - la matematica che ci piace, matematica liceo scientifico

Summary

This video provides a detailed explanation of solving systems of linear equations using Cramer's method, with an emphasis on matrix determinants. The presenter introduces the concept of matrices, which contain numbers that represent coefficients of the system's variables, and explains how to calculate the determinants of these matrices. Through a series of step-by-step calculations, the solution to the system is found, showing how the variables are solved using Cramer's formulas. The method is presented as a mix of challenging but fun mathematical exploration, offering both conceptual clarity and practical examples.

Takeaways

• 😀 Kramer’s method can seem complex, but it's actually a fun and mysterious puzzle to solve, almost like a crossword challenge.
• 😀 The concept of matrices is introduced, though the mathematical theory behind them is not the focus of the discussion.
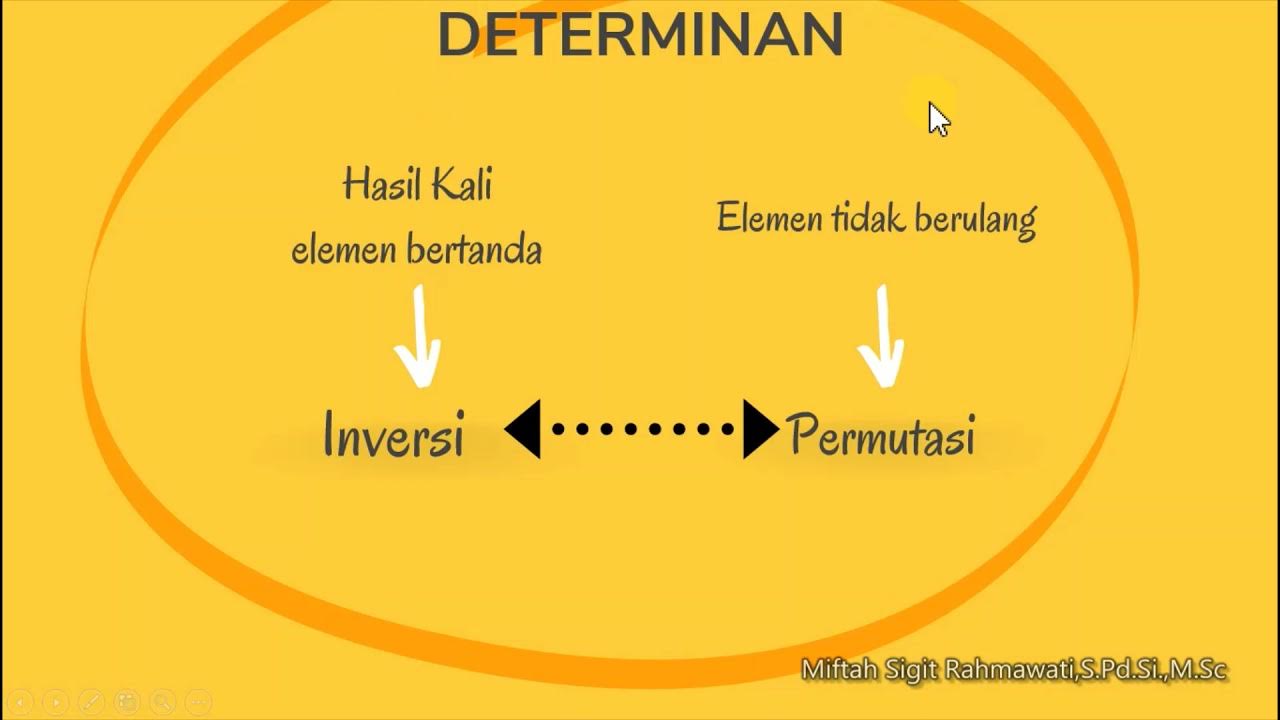
• 😀 A matrix is a collection of numbers, and from these matrices, you can calculate something called a 'determinant'.
• 😀 The matrix for solving the system of equations is formed by the coefficients of the variables and the constants.
• 😀 The solution to the system of equations is achieved by calculating determinants for matrices related to the variables (x, y) and constants.
• 😀 The process involves three key determinants: for x, y, and the original system, denoted as dx, dy, and the determinant of the matrix.
• 😀 Determinants are calculated by multiplying the diagonals of the matrix and subtracting the result of the cross-diagonal multiplication.
• 😀 The determinant of the matrix is computed in a step-by-step manner, showing how to multiply and subtract the necessary numbers.
• 😀 The determinants for dx, dy, and the system are calculated to eventually determine the values of x and y in the system.
• 😀 The final solutions for x and y are easily found once all the determinants are computed and divided accordingly.
• 😀 The speaker reassures that even if students haven’t fully grasped the topic, it’s possible to demonstrate understanding by following the steps.

Q & A

What is the main topic discussed in the transcript?

The main topic is the application of Cramer's method for solving systems of linear equations, with a focus on using matrices and their determinants.

What are matrices in the context of this script?

Matrices are mathematical objects that contain numbers, and in this case, they are used to represent the coefficients of the system of linear equations.

What is the determinant in this context?

A determinant is a value calculated from a square matrix, and it is used to solve the system of linear equations using Cramer's method.

How are the coefficients used in the matrices for Cramer's method?

The coefficients of the system's variables are placed into the matrix, and the determinants of modified matrices are calculated to find the values of the variables.

What is the formula for solving for x and y in Cramer's method?

The formulas are x = dx / determinant, and y = dy / determinant, where dx and dy are determinants of modified matrices, and the determinant is the original matrix's determinant.

What is the role of the matrix with the 'terms not' in Cramer's method?

The matrix with the 'terms not' (constant terms) is used in place of the coefficients in the modified matrices to calculate the new determinants (dx and dy).

Why is Cramer's method described as 'more complex' or 'more tricky'?

Cramer's method can be seen as complex due to the multiple steps involved in calculating the determinants, which might seem cumbersome compared to other methods like substitution or elimination.

What is the determinant calculation process as explained in the script?

To calculate the determinant of a 2x2 matrix, multiply the elements along the main diagonal, subtract the product of the elements along the other diagonal, and then take the difference.

How do you calculate the determinant of dx and dy?

To calculate the determinant of dx, replace the coefficients of x with the constant terms and then calculate the determinant. For dy, replace the coefficients of y with the constant terms and then calculate the determinant.

How does the script ensure accuracy in the determinant calculations?

The script emphasizes the importance of following the correct steps in order, ensuring that the coefficients and constants are correctly placed in the matrices, which leads to accurate determinant calculations.