SLAM C 01
Summary
TLDRThis script discusses the challenges of accurately tracking a robot’s position, particularly the divergence between trajectories generated by wheel counters and external sensors like a laser scanner. The issue arises from calibration errors and random movement uncertainties. The solution involves using probabilistic models to represent these uncertainties and adjust the robot’s trajectory. The script delves into systematic vs. random errors, the concept of probability distributions for position estimation, and how these models can be implemented to simulate the robot's movement and improve positioning accuracy. The script also includes implementation details for creating and manipulating these distributions.
Takeaways
- 😀 The robot's trajectory can be obtained through two methods: external measurement systems and wheel counters.
- 😀 When the robot moves straight, the trajectories from both methods align, but when the robot turns, a drift occurs.
- 😀 The cause of the trajectory divergence is likely due to an incorrect calibration constant, particularly the robot's width.
- 😀 The drift can be partially corrected by adjusting the robot's calibration parameters, but the issue remains if only wheel counters are used.
- 😀 The robot's position can be refined using additional data from a laser scanner, which helps in correcting the robot's position based on a map of cylinders.
- 😀 Systematic errors are predictable and can be corrected by adjusting parameters, while random errors are harder to model and remain uncertain.
- 😀 In modeling, a balance must be found between capturing the most important real-world effects and accounting for random errors that cannot be modeled.
- 😀 A movement model can be used for predicting the robot’s position, but even with this model, real-world errors will still occur.
- 😀 Probability distributions are used to model the uncertainty in the robot’s position, where the likelihood of being at a particular position is expressed as a probability.
- 😀 The distribution class can be manipulated using functions like `move`, `normalize`, and `plot_list` to adjust and visualize how the distribution of probabilities changes over time.
Q & A
What is the main focus of Unit C in the transcript?
-The main focus of Unit C is filtering, specifically addressing how a robot's trajectory can be improved using a combination of wheel counters and laser scanners to correct position errors and systematic drift.
Why do the red and blue trajectories diverge when the robot turns?
-The divergence occurs due to a likely incorrect calibration constant, specifically the width of the robot. This affects the accuracy of the robot's position when turning, as the wheel counter measurements become less reliable.
What is the proposed solution to correct the robot's position?
-The proposed solution is to use a laser scanner in addition to the wheel counters. The laser scanner can identify known features in the environment (such as cylinders) and adjust the robot's position by matching these features to a pre-existing map.
What is the difference between systematic error and random error in the context of the robot's trajectory?
-Systematic error refers to a consistent deviation from the true trajectory due to incorrect modeling or calibration, such as the robot's width. Random error, on the other hand, is caused by unpredictable variations like noise in measurements.
How can the systematic error in the robot's trajectory be corrected?
-The systematic error can be corrected by adjusting the robot's width parameter. However, this approach may not fully eliminate the error, especially if other unmodeled factors, such as slip between the caterpillar tracks and the ground, affect the robot's motion.
What challenges arise when trying to model the robot's motion accurately?
-Modeling the robot's motion accurately is challenging because real-world conditions, such as varying terrain and slipping, introduce factors that are difficult to account for in a simple model. Additionally, every robot will behave differently based on its design and environment.
What is a random error, and how is it represented in the script?
-A random error refers to unpredictable variations in the robot's movement. In the script, it is modeled as a probability distribution, where the robot's actual position is uncertain and spread across a range of possible positions, with varying likelihoods.
How is a discrete probability distribution used to model the robot's position?
-A discrete probability distribution is used to represent the uncertainty in the robot's position. Each position is assigned a probability, and as the robot moves, this distribution is updated to reflect the new range of possible positions based on the movement.
What function should be implemented to move the probability distribution?
-The `move` function should be implemented to shift the probability distribution by a given distance (delta). This function updates the distribution's offset, effectively moving the entire distribution without altering its shape.
What role does the `normalize` function play in the `Distribution` class?
-The `normalize` function ensures that the sum of the values in the distribution equals 1. This is important because the values represent probabilities, and the total probability must always be 1 for a valid distribution.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
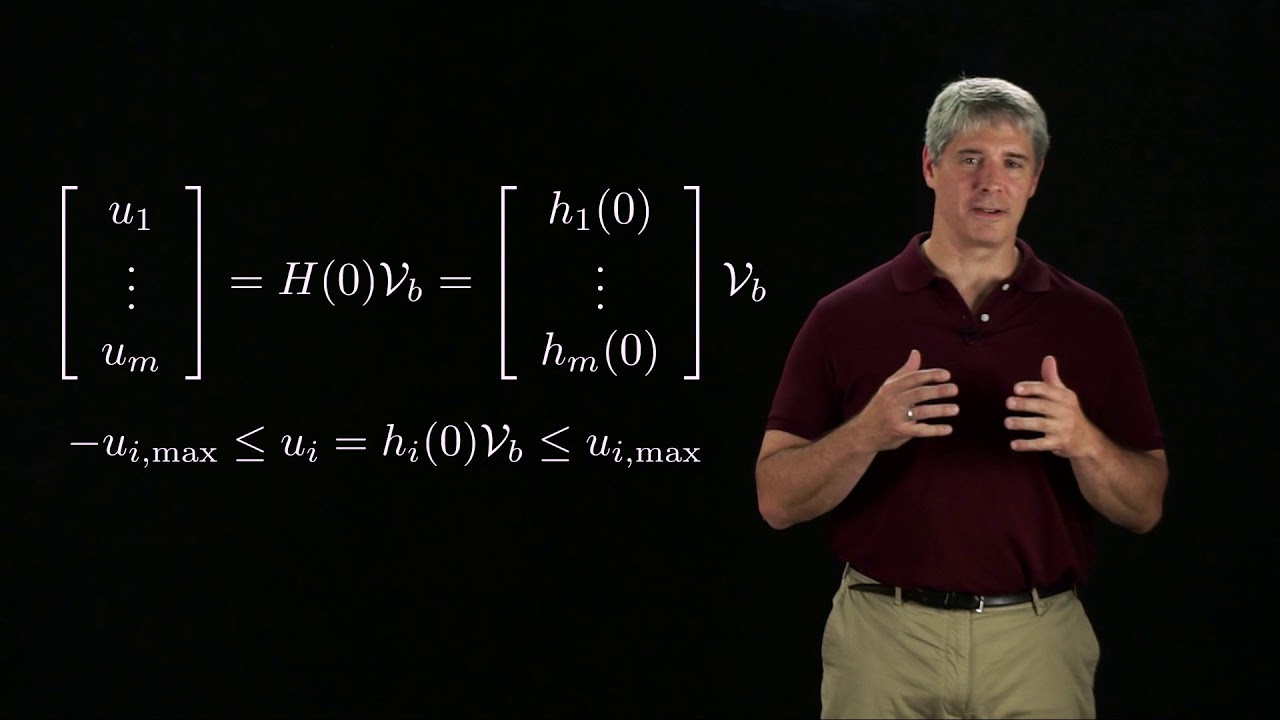
Modern Robotics, Chapter 13.2: Omnidirectional Wheeled Mobile Robots (Part 2 of 2)
What is Hall Effect and How Hall Effect Sensors Work

How to Test ABS Wheel Speed Sensors for Resistance and AC Voltage

What Is LiDAR and how does LiDAR work?

Bagaimana Cara Kerja Scroll Whell Pada Mouse?
Cara Menggunakan Scanner/menghapus Trouble Code menggunakan Scanner G-Scan 2
5.0 / 5 (0 votes)