02 Klasifikasi data statistika

Summary

This video explains the fundamental concepts of statistical data types and measurement scales. It distinguishes between qualitative (categorical) and quantitative (numerical) data, with examples such as food menu items and prices. The video then delves into the four measurement scales: nominal, ordinal, interval, and ratio. These scales are used to categorize, order, and perform mathematical operations on data, with ratio scales allowing the broadest range of operations. Viewers will gain a clear understanding of data classification and measurement in statistics, key for interpreting and analyzing various data sets.

Takeaways

• 😀 Qualitative data refers to non-numerical information, such as attributes or labels (e.g., food names like 'nasi goreng' or 'nasi timbel').
• 😀 Quantitative data involves numerical values derived from measurements or calculations (e.g., prices, temperatures).
• 😀 The two main types of data in statistics are qualitative (categorical) and quantitative (numerical).
• 😀 Qualitative data includes categories that cannot undergo mathematical operations, such as 'Honda' vs 'Toyota' for car brands.
• 😀 Quantitative data, such as price or temperature, can undergo mathematical operations like addition, subtraction, and more.
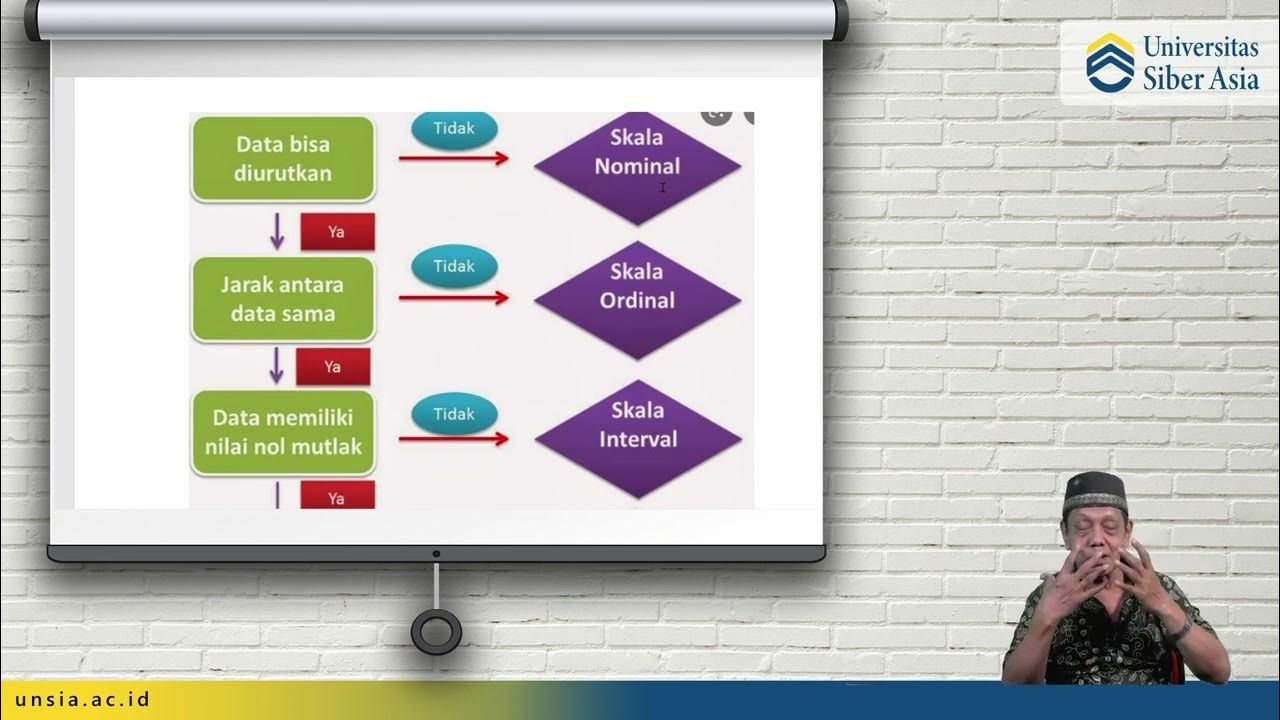
• 😀 The nominal scale categorizes data by labels or names, with no mathematical operations possible (e.g., city names like 'Semarang').
• 😀 The ordinal scale organizes data into ranks or order, but the intervals between ranks are not meaningful (e.g., satisfaction levels).
• 😀 The interval scale allows data to be measured with equal intervals, but lacks a true zero point, preventing multiplication or division (e.g., Celsius temperature).
• 😀 The ratio scale has a true zero point, meaning ratios can be calculated, and it allows for all mathematical operations (e.g., weight, age).
• 😀 Key differences between the scales: nominal data is categorical, ordinal data is ranked, interval data has equal intervals but no absolute zero, and ratio data has both equal intervals and a true zero point.
• 😀 Understanding the measurement scale of data helps determine what types of mathematical operations can be applied and how to interpret the data.

Q & A

What are the two main types of data in statistics?

The two main types of data in statistics are qualitative data and quantitative data.

What is qualitative data and what are some examples?

Qualitative data refers to non-numeric data, often associated with attributes or labels. Examples include vehicle brands (e.g., Honda, Toyota), student names, and city names (e.g., Semarang, Bandung).

What is quantitative data and what are some examples?

Quantitative data refers to numeric data that results from counting or measuring. Examples include prices (e.g., Rp25,000), weights (e.g., 65 kg), and temperatures (e.g., 32°C).

What is the difference between nominal and ordinal scales?

The nominal scale categorizes data without any order or hierarchy (e.g., vehicle brands). The ordinal scale, on the other hand, allows data to be categorized and ordered based on rank or preference (e.g., satisfaction levels like 'very satisfied' or 'unsatisfied').

What is the nominal scale of measurement, and can mathematical operations be performed on it?

The nominal scale categorizes data into distinct groups based on attributes or labels (e.g., vehicle brands, city names). No mathematical operations can be performed on nominal data.

What is the ordinal scale, and can mathematical operations be performed on it?

The ordinal scale allows data to be ordered or ranked but does not provide measurable differences between values (e.g., rankings of students in a class). Mathematical operations, except for ordering, cannot be performed on ordinal data.

What distinguishes the interval scale from other scales in terms of mathematical operations?

The interval scale allows for ordering and measuring the differences between data points (e.g., temperature in Celsius), but it does not have a true zero point. While you can calculate differences, you cannot perform multiplication or division.

What is the ratio scale, and how does it differ from the interval scale?

The ratio scale is similar to the interval scale, but it has a true zero point, which means you can perform all mathematical operations, including multiplication and division (e.g., weight, age). The ratio scale allows meaningful comparisons like 'twice as much' or 'half as much'.

Can you provide an example of data using the ratio scale and explain why it qualifies as ratio data?

An example of ratio data is a child's age, such as 7 years old. The zero point in this case represents the absence of age, and mathematical operations like 'twice as old' are meaningful.

How does the temperature scale (e.g., 32°C) illustrate the limitations of the interval scale?

The temperature scale (e.g., 32°C) is an example of interval data because it measures differences between values, but it lacks a true zero point. For instance, 0°C doesn't mean the absence of temperature. Therefore, while you can measure temperature differences, you cannot say one temperature is 'twice as hot' as another.