Support Vector Machines - THE MATH YOU SHOULD KNOW
Summary
TLDRThis video explains the versatility of Support Vector Machines (SVMs), focusing on their ability to classify both linear and nonlinear data. The key feature that makes SVMs powerful is the kernel trick, which allows the transformation of data into higher-dimensional spaces without explicitly computing the transformation. The video also covers how SVMs use hyperplanes to separate data with maximum margin and how slack variables manage misclassification to avoid overfitting. With the introduction of the dual formulation, SVMs can efficiently handle complex decision boundaries, making them a popular choice for classification problems.
Takeaways
- 😀 SVMs are widely used because of their versatility, handling both linear and non-linear classification problems effectively.
- 😀 The core idea of SVM is to find a hyperplane that maximizes the margin between two classes, leading to fewer misclassifications.
- 😀 SVM uses the kernel trick to map data into higher-dimensional spaces, enabling it to solve non-linear classification problems.
- 😀 The decision boundary (hyperplane) is determined by support vectors, the data points closest to the hyperplane.
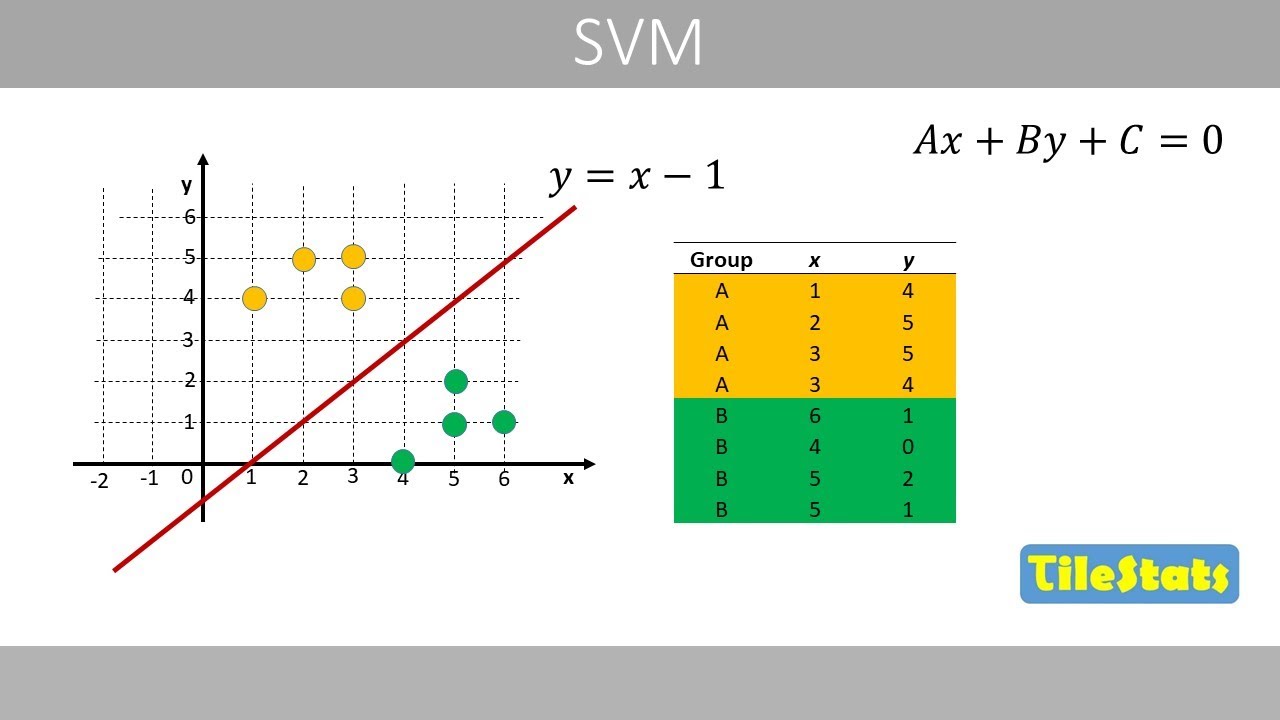
- 😀 In perfectly separable data, the optimal hyperplane is the one that maximizes the margin between classes.
- 😀 Slack variables are introduced to handle non-perfect separation in real-world data, allowing the model to make some mistakes.
- 😀 The hyperparameter 'C' controls the trade-off between maximizing margin and minimizing classification errors (penalties).
- 😀 SVM's optimization problem is typically solved using a primal and dual formulation, with the dual helping eliminate the complex feature transformations.
- 😀 Lagrange multipliers are used in the dual formulation to simplify the optimization process, making it computationally feasible.
- 😀 The kernel function substitutes the complex transformation of data, allowing SVM to work with non-linearly separable data using simpler calculations.
- 😀 After solving the dual formulation, predictions are made by evaluating new data points against the support vectors and decision boundary.
Q & A
Why are Support Vector Machines (SVMs) so popular for classification tasks?
-SVMs are popular because they are powerful classifiers that can handle both linear and nonlinear decision boundaries. They are versatile and can effectively find an optimal separating hyperplane with a maximum margin, which makes them robust for classification tasks.
What is the kernel trick, and why is it important for SVMs?
-The kernel trick allows SVMs to classify data that isn't linearly separable by transforming the data into a higher-dimensional space. This enables SVMs to find a hyperplane that separates the classes in this new space, making them effective even with complex, nonlinear data.
What does it mean to have a 'perfectly separable' dataset, and how does SVM handle it?
-A perfectly separable dataset means that there exists a hyperplane that can separate the data points of different classes without any errors. In such cases, SVM tries to find the hyperplane that maximizes the margin (distance) between the closest points of the two classes.
What role do slack variables play in SVM, and why are they necessary?
-Slack variables are introduced in SVM when data is not perfectly separable. They allow some misclassification to occur, helping the model avoid overfitting. By controlling the size of these slack variables, SVM can balance between underfitting and overfitting.
How does the hyperparameter 'C' affect the performance of an SVM?
-'C' controls the trade-off between achieving a high margin and allowing some misclassification. A low C allows more misclassification (leading to simpler decision boundaries and possible underfitting), while a high C penalizes misclassification heavily (leading to more complex boundaries and potential overfitting).
What is the difference between the primal and dual formulations in SVM?
-The primal formulation is the original optimization problem that includes the feature vectors and the slack variables. The dual formulation, on the other hand, is derived by using Lagrange multipliers to rewrite the problem in terms of dual variables, which allows SVM to operate more efficiently by using kernels.
Why is it challenging to solve the primal form of SVM optimization directly?
-It's challenging because the primal form involves complex transformations of the input data into a higher-dimensional space (Phi), which can be computationally expensive and difficult to handle directly.
What is a kernel function, and how does it simplify SVM computations?
-A kernel function is a mathematical function that allows the inner product of feature vectors in a higher-dimensional space to be computed without explicitly mapping the data into that space. This simplifies computation and enables SVMs to handle nonlinear data without the need for complex feature transformations.
How does SVM make predictions once the model has been trained?
-Once trained, SVM makes predictions by computing the inner product between the test feature vector and the support vectors, using the learned weights and bias. This can be done efficiently by applying the kernel function, which eliminates the need to directly compute in the high-dimensional space.
What types of kernel functions are commonly used with SVMs, and why?
-Common kernel functions used with SVMs include the Radial Basis Function (RBF) and Gaussian kernels. These are popular because they can model complex, nonlinear relationships between data points, enabling SVMs to handle data that isn't linearly separable.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
Support Vector Machines (SVM) - the basics | simply explained

Support Vector Machines Part 1 (of 3): Main Ideas!!!

Support Vector Machine: Pengertian dan Cara Kerja

LA01_Vectors

Correlation Doesn't Equal Causation: Crash Course Statistics #8

Struktur Data (Tree & Graph ) | Elemen Berpikir Komputasional | Materi Informatika Kelas 9 Fase D
5.0 / 5 (0 votes)