Elipse trazado y elementos | Introducción
Summary
TLDREn este tutorial, se explica de manera clara y visual el concepto de la elipse, su definición y los elementos que la componen. Se muestra cómo la suma de las distancias desde cualquier punto de la elipse hasta dos puntos fijos (los focos) es constante. Se detallan elementos como los focos, los vértices, los ejes mayor y menor, y cómo la aplicación del teorema de Pitágoras relaciona estas distancias. El vídeo incluye una demostración práctica de la construcción de la elipse y cómo se pueden aplicar estas fórmulas en ejercicios posteriores.
Takeaways
- 😀 La elipse es el lugar geométrico de los puntos cuya suma de distancias a dos puntos fijos, llamados focos, es constante.
- 😀 Los focos son los dos puntos fijos que determinan la forma de la elipse.
- 😀 Se utiliza una cuerda de 24 centímetros para trazar la elipse, asegurando que la suma de las distancias a los dos focos sea siempre 24 cm.
- 😀 Los puntos que cumplen con la condición de la suma constante de distancias forman la elipse.
- 😀 La elipse tiene dos ejes: el eje mayor (2a) y el eje menor (2b), siendo el eje mayor la distancia entre los vértices más lejanos.
- 😀 El centro de la elipse está en el punto medio entre los dos focos.
- 😀 Los vértices son los puntos donde la elipse intersecta el eje focal, y su distancia al centro es 'a'.
- 😀 La distancia entre el centro y los focos se denomina 'c', y la distancia entre un foco y un vértice es 'a'.
- 😀 La elipse puede ser dividida en dos mitades por su eje focal y un eje perpendicular, cada una de las cuales es simétrica.
- 😀 Aplicando el teorema de Pitágoras, se puede obtener la relación entre los ejes mayor y menor, ya que la distancia 'c' (centro a foco) y 'b' (eje menor) forman un triángulo rectángulo con 'a' (eje mayor).
Q & A
¿Qué es una elipse?
-Una elipse es el lugar geométrico de los puntos cuya suma de distancias a dos puntos fijos, llamados focos, es constante.
¿Qué son los focos en una elipse?
-Los focos son dos puntos fijos en los que se basa la definición de la elipse, y la suma de las distancias desde cualquier punto de la elipse hasta estos dos focos es constante.
¿Cómo se puede trazar una elipse de forma física?
-Se puede trazar una elipse usando un trozo de hilo o pita atado a los dos focos. A medida que se mueve un punto sobre la pita, la suma de las distancias a los focos siempre será constante.
¿Qué es el eje focal en una elipse?
-El eje focal es la recta que pasa por los dos focos de la elipse. Es el eje principal que conecta ambos focos.
¿Cómo se llama la distancia entre el centro y los focos en una elipse?
-La distancia entre el centro y un foco se llama 'c', y se utiliza para calcular la relación entre los elementos de la elipse.
¿Qué es el centro de una elipse?
-El centro de la elipse es el punto medio entre los dos focos, y es el punto de intersección de los ejes mayor y menor.
¿Qué son los vértices de la elipse?
-Los vértices de la elipse son los puntos donde la elipse intersecta el eje mayor. Los vértices más alejados se encuentran a una distancia de 2a entre sí.
¿Qué es el eje mayor y cómo se relaciona con la elipse?
-El eje mayor es la distancia más larga de la elipse, que se extiende entre los dos vértices más distantes. Su longitud es 2a.
¿Qué es el eje menor en una elipse?
-El eje menor es la distancia más corta de la elipse, perpendicular al eje mayor. Su longitud es 2b.
¿Cómo se aplica el teorema de Pitágoras en una elipse?
-El teorema de Pitágoras se aplica en un triángulo rectángulo formado por el centro, un vértice y un punto en el eje menor. La fórmula resultante es: a² = b² + c².
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
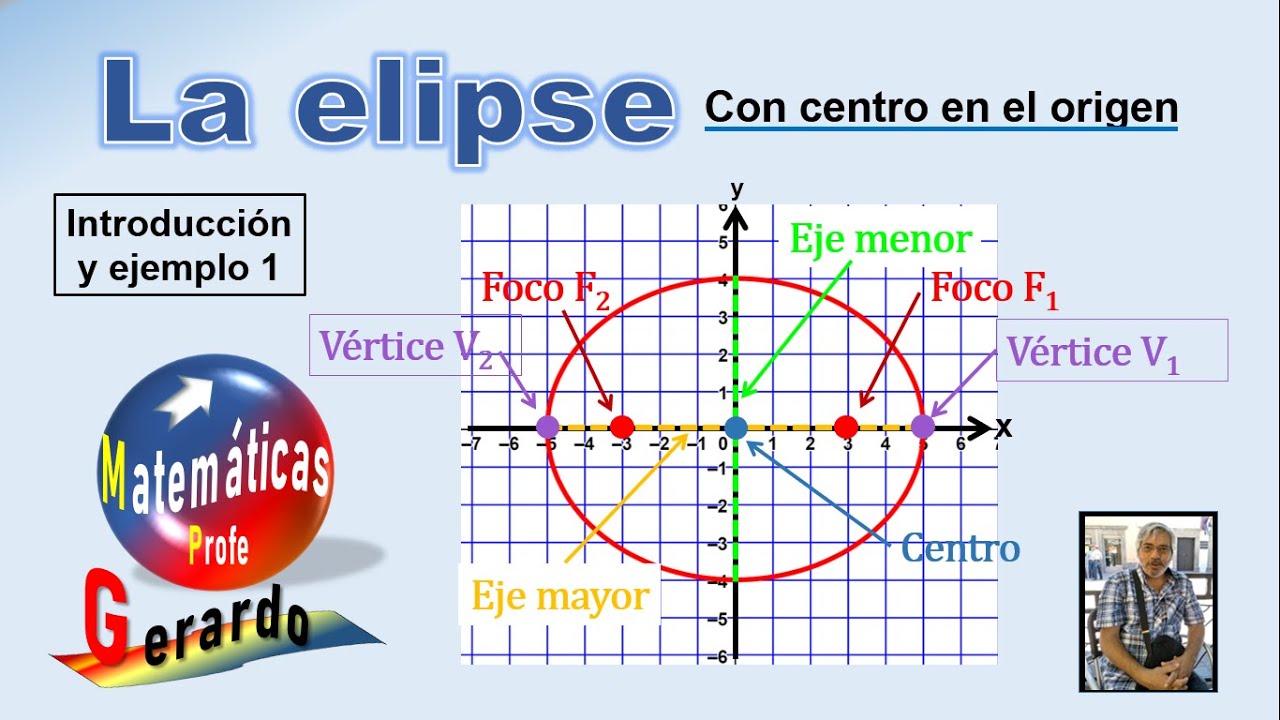
La elipse con centro en el origen. Introducción y ejemplo 1.

✅ELIPSE con centro FUERA del ORIGEN [100% 𝙀𝙛𝙚𝙘𝙩𝙞𝙫𝙤 😎🫵💯] Geometría Analítica

ONDAS Nº 1: Las Ondas y sus Elementos .....

🏉 ELIPSE: Concepto y elementos (focos, vértices, Eje Mayor, Eje Menor, L.R.) | Juliana la profe

HALLAR LA EXCENTRICIDAD Y LA ECUACIÓN DE UNA ELIPSE

✅ 2 ARTICULACIONES | QUE SON | TIPOS | CLASIFICACIÓN (Facil Rapido Sencillo)
5.0 / 5 (0 votes)
