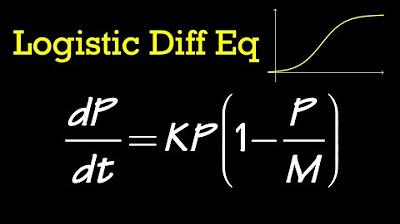9.4 - Models for Population Growth

Summary

This video explains two key models for population growth: the law of natural growth and the logistic model. It discusses how the law of natural growth, which assumes population growth is proportional to size, leads to exponential growth. However, real-world population growth is often limited by factors such as resources, leading to the logistic model. This model introduces a carrying capacity, showing that populations eventually stabilize. The video also covers the derivation and application of the logistic equation, including how to calculate population growth over time, and highlights the point where the fastest rate of growth occurs.

Takeaways

• 😀 The logistic growth model is used to predict population changes over time, factoring in a carrying capacity.
• 😀 The population growth formula involves initial population, carrying capacity, growth rate, and time.
• 😀 The formula for logistic growth requires the use of natural logarithms, which introduces approximation when rounding irrational numbers.
• 😀 Using approximate values for constants in the logistic growth formula can lead to slightly less accurate but more manageable calculations.
• 😀 To find the population at a specific time, such as after 3 years, we substitute time into the logistic growth formula.
• 😀 After three years, using the logistic growth formula, the population reaches 7,500 deer.
• 😀 The logistic model suggests that population growth accelerates initially but slows down as the population approaches carrying capacity.
• 😀 The maximum growth rate occurs when the population is half of the carrying capacity, such as at 5,000 deer in this example.
• 😀 The rate of population growth decreases as the population nears its carrying capacity due to limited resources and space.
• 😀 The homework will involve demonstrating that the maximum rate of growth happens at half the carrying capacity using differential equations.
• 😀 The key focus in applying the logistic growth model is understanding how population dynamics change over time, particularly near the carrying capacity.

Q & A

What is the logistic growth model used in the transcript?

The logistic growth model described in the transcript is used to model the population growth of a species, taking into account a carrying capacity. It is represented by the formula P(t) = K / (1 + (K - P0)/P0 * e^(-rt)), where K is the carrying capacity, P0 is the initial population, r is the growth rate, and t is time.

What is the purpose of the natural logarithm calculation mentioned in the transcript?

The natural logarithm calculation is used to solve for the growth rate (r) in the logistic growth model. It involves taking the logarithm of the expression 1/3, which requires rounding to an approximation since the result is an irrational number.

Why is the speaker using approximations in the logistic model calculations?

The speaker uses approximations because the natural logarithm of 1/3 is an irrational number, meaning it cannot be expressed exactly. When solving for values like the growth rate, rounding is necessary, but this introduces a small degree of inaccuracy.

How does the logistic growth model calculate the population after three years?

To calculate the population after three years, the speaker plugs in 3 for time (t) into the logistic growth equation. The resulting population is calculated as 7,500 deer after three years, based on the given model and parameters.

What is the maximum growth rate in the logistic model, and when does it occur?

The maximum rate of growth in the logistic model occurs when the population is exactly half of the carrying capacity. In the example, the carrying capacity is 10,000, so the fastest growth rate occurs when the population is 5,000.

What happens to the population growth rate as the population approaches the carrying capacity?

As the population approaches the carrying capacity, the growth rate slows down. Initially, growth is fast, but as the population nears the carrying capacity, it decelerates because resources become limited.

How does the speaker explain the importance of keeping exact values versus rounding in solving the logistic model?

The speaker highlights that rounding values introduces approximations, which can reduce the precision of the solution. By keeping exact values as much as possible, such as using the natural logarithm without rounding, the solution remains more accurate.

What is the significance of solving for K in the logistic growth model?

Solving for K (the carrying capacity) is important because it provides an upper limit to the population that the model predicts will be reached. It represents the maximum sustainable population that can be supported by the environment.

How is the population model set up in the transcript for the specific case with deer?

In the specific deer example, the population growth model is set up with an initial population of 1,000 deer and a carrying capacity of 10,000. The model uses a growth rate based on the fractional factor of 1/3 to describe how the population increases over time.

What is the relationship between the carrying capacity and the growth rate in the logistic model?

In the logistic growth model, the carrying capacity (K) influences the growth rate. As the population approaches the carrying capacity, the growth rate slows down. The growth rate is fastest when the population is at half of the carrying capacity, and it gradually decreases as the population nears the maximum limit.