Activation Functions - EXPLAINED!

Summary

This video provides an insightful overview of activation functions in neural networks, explaining their critical role in enabling networks to learn complex, non-linear patterns. It covers the basics, from simple linear separability to more complicated data structures, and addresses key challenges like the vanishing gradient and dying ReLU problems. The video also discusses various activation functions such as sigmoid, ReLU, and softmax, and how they are applied in different network layers depending on the task (classification or regression). Ultimately, it emphasizes the importance of choosing the right activation function for efficient learning and optimal performance in neural networks.

Takeaways

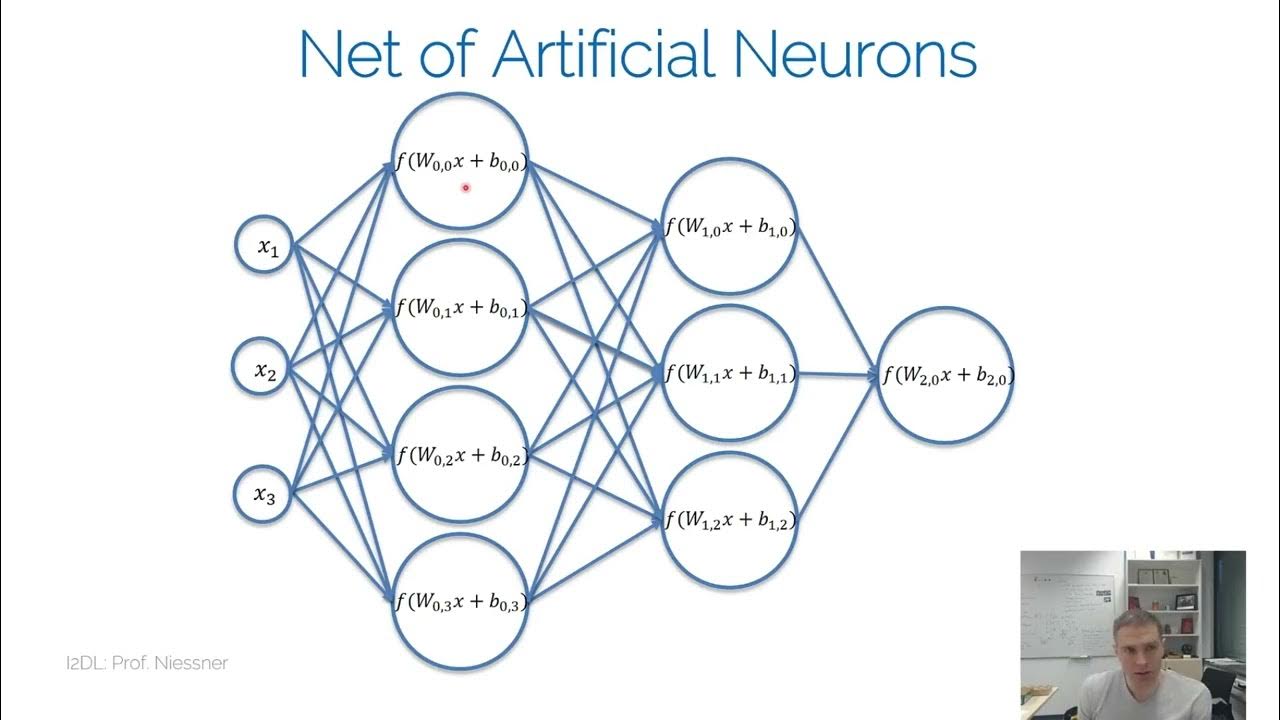
• 😀 Neural networks require activation functions to handle non-linear relationships in data.
• 😀 A simple network with no activation function can only classify data that is linearly separable.
• 😀 The sigmoid function is commonly used but causes the vanishing gradient problem, where gradients become too small for learning to occur.
• 😀 ReLU (Rectified Linear Unit) is a popular solution to the vanishing gradient problem, allowing gradients to flow more easily.
• 😀 The dying ReLU problem occurs when neurons are 'turned off' due to negative inputs, preventing them from learning.
• 😀 Leaky ReLU and ELU (Exponential Linear Unit) are solutions to the dying ReLU problem, allowing for learning even with negative inputs.
• 😀 In classification tasks, the softmax function is used to output probabilities that sum to one, representing the likelihood of each class.
• 😀 In regression tasks, no activation function is typically used in the output layer, allowing for real-valued outputs.
• 😀 Increasing the number of layers in a network can help with more complex data, but care must be taken to choose the right activation function to avoid issues like vanishing gradients.
• 😀 The choice of activation function depends on the complexity of the task, with functions like sigmoid or tanh being suitable for simpler cases, and ReLU and its variants better for deeper networks.

Q & A

What is the purpose of activation functions in neural networks?

Activation functions introduce non-linearity into neural networks, allowing them to model complex patterns and decision boundaries that can't be captured by linear functions alone.

What happens if a neural network doesn't use an activation function?

Without an activation function, the neural network can only model linear relationships between inputs and outputs, limiting its ability to learn more complex patterns.

Why is the sigmoid function prone to the vanishing gradient problem?

The sigmoid function squashes input values into a small range (0 to 1), which leads to very small gradients during backpropagation, making learning slow and potentially halting the network's ability to train effectively.

How does ReLU solve the vanishing gradient problem?

ReLU allows positive values to pass through unaltered and sets negative values to zero, which prevents the gradients from becoming too small during backpropagation, helping the network learn more effectively.

What is the 'dying ReLU' problem?

The dying ReLU problem occurs when a neuron becomes inactive because it only outputs zero for negative inputs. This can happen during training if the bias becomes too negative, causing the neuron to stop learning.

How can the dying ReLU problem be solved?

The dying ReLU problem can be mitigated by using modified versions like Leaky ReLU or Parametric ReLU, which allow small negative values to pass through, ensuring that neurons remain active and continue learning.

What is the role of Softmax in the output layer of a classification network?

Softmax is used in the output layer of classification networks to convert the raw output values into probabilities, which represent the likelihood of each class being the correct one.

Why don't we typically use activation functions in regression problems?

In regression problems, we usually want the output to be a real number, so no activation function is applied to ensure the network can output continuous values without restriction.

What happens when data is more complicated than linearly separable data?

When data is more complex and not linearly separable, we introduce activation functions like sigmoid, tanh, or ReLU to allow the network to create more complex decision boundaries and fit the data more effectively.

How does the sigmoid function compare to a linear equation in terms of decision boundaries?

A sigmoid function introduces non-linearity and can create more complex decision boundaries, such as curves. In contrast, a linear equation results in a straight line, which limits the network's ability to separate more complicated data.