Why Neural Networks can learn (almost) anything

Summary

This script introduces the concept of neural networks as universal function approximators. It begins by explaining functions as a system of inputs and outputs, then explores how neural networks can be trained to reverse-engineer and approximate functions from data. The video demonstrates the mechanics of a neural network, showing how simple building blocks like neurons can be combined to construct complex functions. It emphasizes the importance of non-linearities in allowing neural networks to learn and highlights their ability to approximate any function given enough data and neurons. The script discusses the potential of neural networks to learn and emulate intelligent behavior, while acknowledging practical limitations and the necessity of sufficient training data. It concludes by emphasizing the transformative impact of neural networks in fields like computer vision and natural language processing.

Takeaways

• 🤖 Neural networks are a form of function approximators that can learn to represent complex patterns and relationships in data.
• 🧩 Neural networks are composed of interconnected neurons, which are simple linear functions that can be combined to create more complex non-linear functions.
• 🚀 Neural networks can be trained using algorithms like backpropagation to automatically adjust their parameters and improve their approximation of a target function.
• 🌀 Neural networks can learn to approximate any function to any desired degree of precision, making them universal function approximators.
• 🖼️ Neural networks can learn to approximate functions that represent various tasks, such as image classification, language translation, and more, by encoding inputs and outputs as numerical data.
• 💻 Neural networks are theoretically Turing-complete, meaning they can solve any computable problem, given enough data and resources.
• 🔮 The success of neural networks in approximating functions depends on the availability of sufficient data that accurately represents the underlying function.
• 🚧 Neural networks have practical limitations, such as finite resources and challenges in the learning process, that constrain their ability to approximate certain functions.
• 🤯 Neural networks have revolutionized fields like computer vision and natural language processing by providing a way to solve problems that require intuition and fuzzy logic, which are difficult to manually program.
• 🚀 The humble function is a powerful concept that allows neural networks to construct complex representations and approximate a wide range of intelligent behaviors.

Q & A

What is a neural network learning in this video?

The neural network is learning the shape of the infinitely complex fractal known as the Mandelbrot set.

What is the fundamental mathematical concept that needs to be understood in order to grasp how a neural network can learn?

The fundamental mathematical concept that needs to be understood is the concept of a function, which is informally defined as a system of inputs and outputs.

How can a function be approximated if the actual function itself is unknown?

A function approximator can be used to construct a function that captures the overall pattern of the data, even if there is some noise or randomness present.

What is a neural network in the context of function approximation?

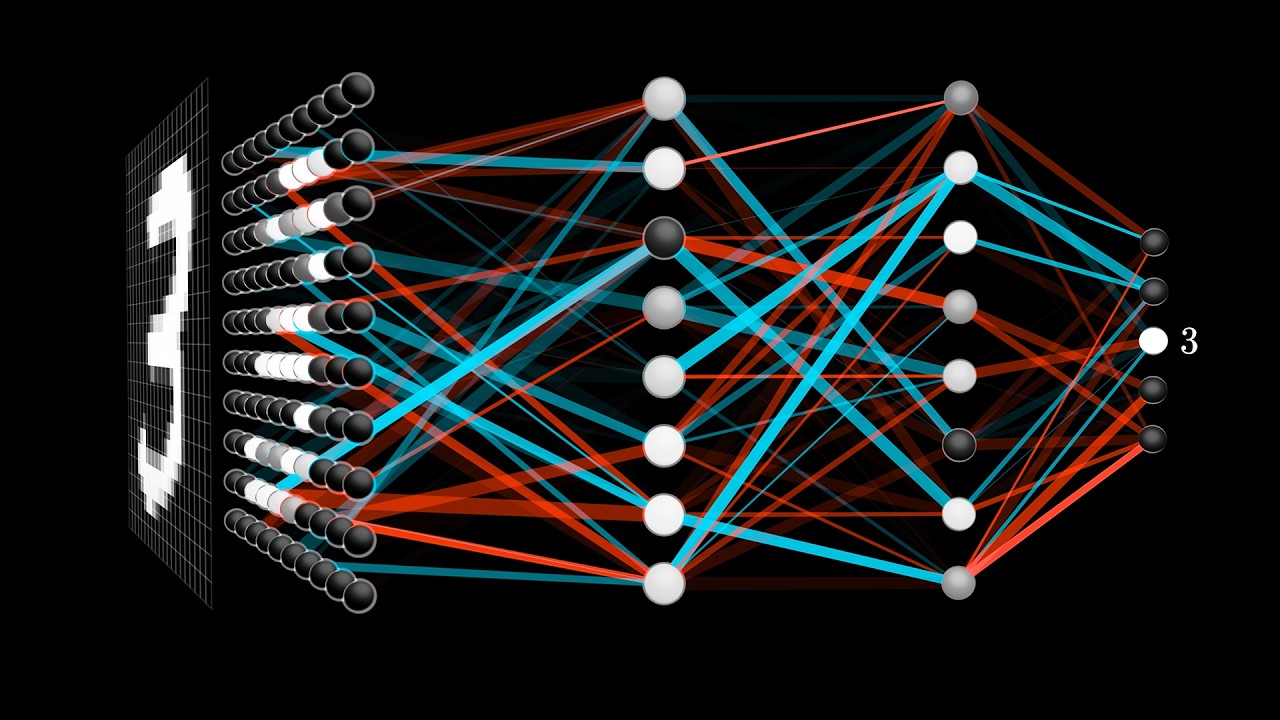
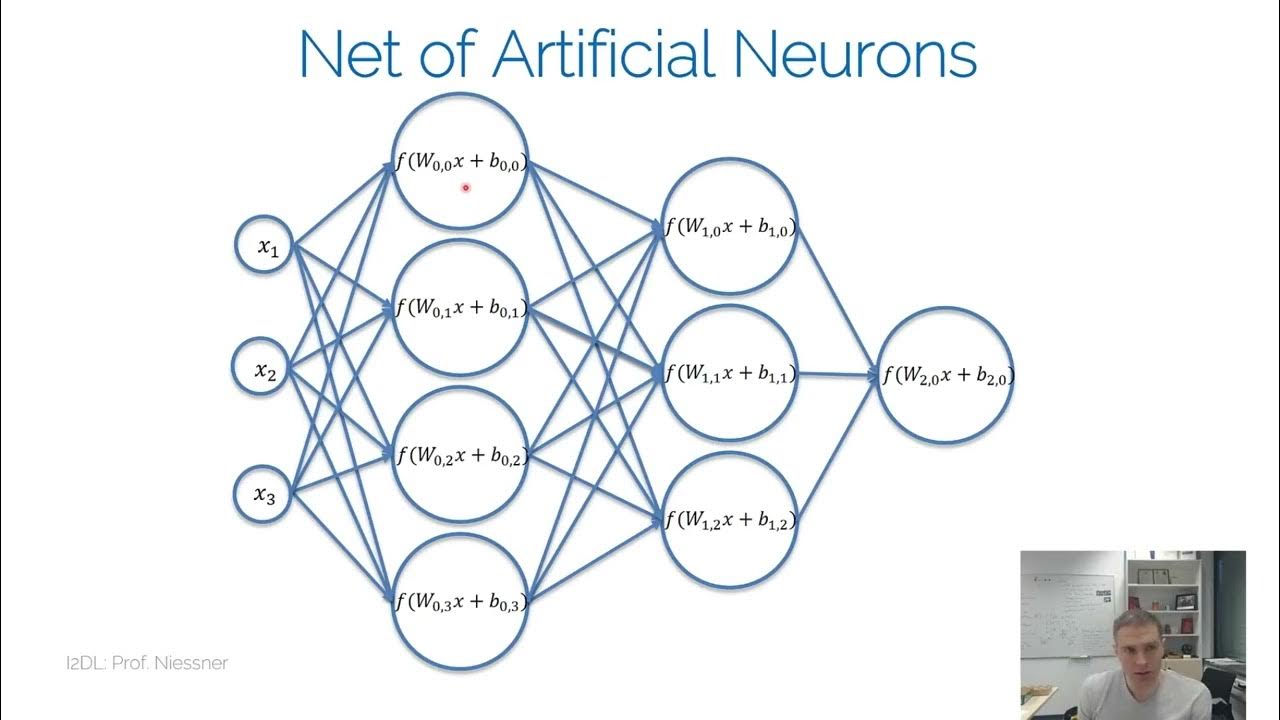
A neural network is a function approximator that can learn to approximate any function by combining simple computations.

What is the basic building block of a neural network?

The basic building block of a neural network is a neuron, which is a simple linear function that takes in inputs, multiplies them by weights, adds a bias, and produces an output.

Why is a non-linearity needed in a neural network?

A non-linearity, such as the rectified linear unit (ReLU), is needed to prevent the neural network from simplifying down to a single linear function, which would limit its ability to learn more complex patterns.

What algorithm is commonly used to automatically tune the parameters of a neural network?

The most common algorithm for automatically tuning the parameters of a neural network is called backpropagation.

Can neural networks learn any function?

Neural networks have been rigorously proven to be universal function approximators, meaning they can approximate any function to any degree of precision, as long as there is enough data to describe the function.

What are some practical limitations of neural networks?

Practical limitations of neural networks include finite network size, constraints introduced by the learning process, and the requirement for sufficient data to accurately approximate the target function.

What are some areas where neural networks have been particularly successful?

Neural networks have been indispensable in fields like computer vision, natural language processing, and other areas of machine learning, where they have been able to learn intuitions and fuzzy logic that are difficult for humans to manually program.

Outlines

00:00

🧠 Neural Network Learning the Mandelbrot Set

This paragraph introduces the video's topic, which is about an artificial neural network learning the shape of the infinitely complex Mandelbrot fractal set. It provides context by explaining what the Mandelbrot set is and emphasizing its complexity. The paragraph then transitions into discussing the fundamental mathematical concept of a function, which is a system that takes inputs and produces outputs. It poses the question of whether it's possible to reverse engineer a function that produced a given data set of inputs and outputs, even if there is some noise or randomness. The concept of a function approximator, which is what a neural network is, is introduced.

05:01

🔄 How Neural Networks Approximate Functions

This paragraph delves deeper into how neural networks work as function approximators. It introduces a visualization tool that demonstrates a neural network taking two inputs (x1 and x2) and producing one output. Through this visual representation, the paragraph explains how the network constructs a shape that accurately distinguishes between different data points, effectively learning and approximating the underlying function that describes the data. The concept of neurons, the building blocks of neural networks, is introduced, with each neuron being a simple linear function that takes inputs, multiplies them by weights, and produces an output. The paragraph then explores the limitations of linear functions and the need for non-linearities, such as the rectified linear unit (ReLU), to overcome these limitations and enable more complex function approximations.

10:03

🔀 Neural Networks as Universal Function Approximators

This paragraph discusses the power of neural networks as universal function approximators, capable of approximating any function to any desired degree of precision. It emphasizes that by adding more neurons and layers, neural networks can piece together even the most complicated approximations, capturing intricate patterns like spirals. The paragraph highlights that neural networks can learn anything that can be expressed as a function, including the infinitely complex Mandelbrot set. It then expands on the concept of encoding various inputs (images, text, audio) as numbers and using neural networks to process them, as they can simulate any processing that can be written as a function. The paragraph also touches on the Turing completeness of neural networks, implying their ability to solve the same kinds of problems that computers can. It concludes by acknowledging some practical limitations and considerations, while emphasizing the transformative impact of neural networks on fields like computer vision and natural language processing.

Keywords

💡Function

A function is a mathematical concept that represents a relationship between inputs and outputs. In the context of the video, a function is described as a system that takes a number (or set of numbers) as input and produces a corresponding output. Functions are central to understanding how neural networks learn, as they can be used to model the relationship between input data (such as images or text) and desired outputs (such as labels or translations). The video explains that neural networks are function approximators, capable of learning to emulate any function that can be expressed as a mapping from inputs to outputs.

💡Neural Network

A neural network is a machine learning model that is inspired by the structure and function of biological neural networks in the brain. It consists of interconnected nodes (called neurons) that are organized into layers. Each neuron receives inputs, performs a calculation on those inputs (using weights and biases), and passes the result to the next layer. Neural networks are capable of learning complex patterns and relationships in data through a process called training, where the weights and biases are adjusted to minimize the difference between the network's output and the desired output (known as the loss function). The video uses a visual tool to demonstrate how a simple neural network can learn to approximate various functions, including complex fractals like the Mandelbrot set.

💡Neuron

In the context of artificial neural networks, a neuron is a fundamental building block that performs a simple mathematical operation. Each neuron takes in multiple inputs, multiplies each input by a weight, sums up the weighted inputs, and applies an activation function to the sum (along with a bias value). The resulting output is then passed to the next layer of neurons. The video explains that individual neurons are essentially linear functions, but when combined in a network and with the application of non-linear activation functions, they can collectively approximate more complex, non-linear functions.

💡Activation Function

An activation function is a mathematical operation applied to the output of a neuron in a neural network. Its purpose is to introduce non-linearity into the network, which allows the model to learn and represent more complex relationships in the data. The video demonstrates how using a simple linear function as the activation function (i.e., no activation function) results in a neural network that cannot accurately approximate the target function. However, when a non-linear activation function (in this case, the Rectified Linear Unit or ReLU) is applied, the network can learn to better approximate the target function. Activation functions are an essential component of neural networks, as they enable the model to capture non-linear patterns and overcome the limitations of individual linear neurons.

💡Back Propagation

Back propagation is a widely used algorithm for training artificial neural networks. It is a method for adjusting the weights and biases of the neurons in a neural network to minimize the difference between the network's output and the desired output (the loss function). Back propagation works by computing the gradient of the loss function with respect to the network's weights and biases and then updating these parameters in the direction that reduces the loss. This process is repeated iteratively, allowing the network to learn and improve its ability to approximate the target function. While the video doesn't go into the technical details of back propagation, it mentions that this algorithm is what powers the learning process demonstrated in the visual tool.

💡Function Approximation

Function approximation is the process of constructing a function (a mathematical model) that closely matches a set of input-output data points. In the context of the video, neural networks are described as function approximators, meaning they have the ability to learn and approximate any function that can be expressed as a mapping from inputs to outputs. The video demonstrates how a neural network can learn to approximate various functions, including simple linear functions, more complex spirals, and even the highly intricate Mandelbrot set fractal. The ability to approximate functions is a fundamental property of neural networks and is what enables them to learn and generalize from data to solve a wide range of problems.

💡Universal Function Approximator

The concept of a universal function approximator refers to a model that can approximate any continuous function to an arbitrary degree of accuracy, given enough complexity and data. The video states that neural networks can be rigorously proven to be universal function approximators, meaning they have the theoretical capacity to approximate any function, no matter how complex, by adding more neurons and layers to the network architecture. This property of neural networks is a key factor in their versatility and success in solving a wide range of problems that can be formulated as mapping inputs to outputs (such as image classification, language translation, and many others). The video illustrates this concept by demonstrating how a neural network can learn to approximate the infinitely complex Mandelbrot set fractal.

💡Turing Completeness

Turing completeness is a concept from computer science that refers to a system's ability to perform any computation that a Turing machine (a theoretical model of a general-purpose computer) can perform. The video mentions that, under certain assumptions, neural networks can be proven to be Turing complete, meaning they have the theoretical capacity to simulate any algorithm or program that can be executed on a conventional computer. This property implies that neural networks have the potential to learn and approximate any computable function, not just those that can be expressed as a simple mapping from inputs to outputs. While the video acknowledges the theoretical limitations and practical constraints of neural networks, it highlights their vast potential as function approximators and their ability to learn complex patterns and behaviors.

💡Machine Learning

Machine learning is a field of artificial intelligence that focuses on developing algorithms and models that can learn and improve from data, without being explicitly programmed for a specific task. Neural networks are a type of machine learning model that can learn patterns and relationships in data through a training process. The video discusses how neural networks can be used to solve various machine learning problems, such as computer vision (e.g., image classification) and natural language processing (e.g., language translation), by learning to approximate the underlying functions that map inputs (like images or text) to desired outputs (like labels or translations). Machine learning has transformed many areas of computer science by enabling systems to develop intuition and learn fuzzy logic that is difficult to manually program.

💡Fractal

A fractal is a geometric pattern that exhibits self-similarity at different scales, meaning that the same or similar patterns are repeated at smaller and smaller scales. The video uses the Mandelbrot set, a famous and infinitely complex fractal, as an example of a function that a neural network can learn to approximate. Fractals are often used to illustrate the concept of universal function approximation because their intricate and recursive structure represents a highly complex function that would be challenging to model using traditional mathematical methods. The ability of neural networks to learn and approximate fractals like the Mandelbrot set demonstrates their power as function approximators, capable of capturing intricate patterns and relationships in data.

Highlights

A neural network is learning the shape of the infinitely complex fractal known as the Mandelbrot set.

A function is a system of inputs and outputs - numbers in, numbers out.

If we know some of a function's inputs and outputs, but not the function itself, we can reverse engineer the function that produced the data.

A neural network is a function approximator that can construct a function to describe a data set, even with some noise or randomness.

A neuron is a function that takes inputs, multiplies them by weights, adds a bias, and produces a single output.

A neural network is a network of neurons, where each neuron's output becomes the input for the next layer of neurons.

Neurons are the building blocks of a neural network, and they can be combined to construct more complicated functions.

Linear functions can only combine to make a single linear function, which is not sufficient for approximating complex data.

Adding a non-linearity, such as the rectified linear unit (ReLU) activation function, allows neurons to overcome their individual limitations and build more complex functions.

Backpropagation is the most common algorithm for automatically adjusting the weights and biases of a neural network to improve its function approximation.

Neural networks can be proven to be universal function approximators, capable of approximating any function to any desired degree of precision.

Neural networks can learn any intelligent behavior, process, or task that can be expressed as a function, including computer vision, natural language processing, and other machine learning problems.

Under certain assumptions, neural networks are Turing complete, meaning they can solve the same types of problems as any computer and can learn to simulate any algorithm.

Practical limitations, such as network size, learning process constraints, and availability of sufficient training data, can restrict what neural networks can learn.

Neural networks have transformed fields like computer vision and natural language processing by providing a way to solve problems that require intuition and fuzzy logic, which are difficult to manually program.

Transcripts

you are currently watching an artificial

neural network learn

in particular it's learning the shape of

an infinitely complex fractal known as

the mandelbrot set

this is what that set looks like

complexity all the way down

now in order to understand how a neural

network can learn the mandelbrot set

really how it can learn anything at all

we will need to start with a fundamental

mathematical concept

what is a function

informally a function is just a system

of inputs and outputs numbers in numbers

out

in this case you input an x and it

outputs a y

you can plot all of a function's x and y

values in a graph where it draws out a

line what is important is that if you

know the function you can always

calculate the correct output y given any

input x

but say we don't know the function and

instead only know some of its x and y

values we know the inputs and outputs

but we don't know the function used to

produce them

is there a way to reverse engineer that

function that produced this data

if we could construct such a function we

could use it to calculate a y value

given an x value that is not in our

original data set this would work even

if there was a little bit of noise in

our data a little randomness we can

still capture the overall pattern of the

data and continue producing y values

that aren't perfect but close enough to

be useful what we need is a function

approximation and more generally a

function approximator

that is what a neural network is

this is an online tool for visualizing

neural networks and i'll link it in the

description below this particular

network takes two inputs x1 and x2 and

produces one output technically this

function would create a

three-dimensional surface but it's

easier to visualize in two dimensions

this image is rendered by passing the x

y coordinate of each pixel into the

network which then produces a value

between negative one and one that is

used as the pixel value these points are

our data set and are used to train the

network when we begin training it

quickly constructs a shape that

accurately distinguishes between blue

and orange points building a decision

boundary that separates them it is

approximating the function that

describes the data it's learning and is

capable of learning the different data

sets that we throw at it

so what is this middle section then well

as the name implies this is the network

of neurons each one of these nodes is a

neuron which takes in all the inputs

from the previous layer of neurons and

produces one output which is then fed to

the next layer

inputs and outputs sounds like we're

dealing with a function

indeed a neuron itself is just a

function one that can take any number of

inputs and has one output each input is

multiplied by a weight and all are added

together along with bias the weights and

bias make up the parameters of this

neuron values that can change as the

network learns

to keep it easy to visualize we'll

simplify this down to a two-dimensional

function with only one input and one

output

now neurons are our building blocks of

the larger network building blocks that

can be stretched and squeezed and

shifted around and ultimately work with

other blocks to construct something

larger than themselves the neuron as

we've defined it here works like a

building block it is actually an

extremely simple linear function one

which forms a flat line or plane when

there's more than one input

with the two parameters the weight and

bias we can stretch and squeeze and move

our function up and down and left and

right

as such we should be able to combine it

with other neurons to form a more

complicated function one built from lots

of linear functions

so let's start with a target function

one we want to approximate i've

hard-coded a bunch of neurons whose

parameters were found manually and if we

weight each one and add them up as would

happen in the final neuron of the

network we should get a function that

looks like the target function

well that didn't work at all what

happened

well if we simplify our equation

distributing weights and combining like

terms we end up with a single linear

function

turns out linear functions can only

combine to make one linear function this

is a big problem because we need to make

something more complicated than just a

line we need something that is not

linear a non-linearity

in our case we will be using a relu a

rectified linear unit we use it as our

activation function meaning we simply

apply it to our previous naive neuron

this is about as close as you can get to

a linear function without actually being

one and we can tune it with the same

parameters as before

however you may notice that we can't

actually lift the function off of the

x-axis which seems like a pretty big

limitation

well let's give it a shot anyway and see

if it performs any better than our

previous attempt

we're still trying to approximate the

same function and we're using the same

weights and biases as before but this

time we're using a value as our

activation function

and just like that the approximation

looks way better unlike before our

function cannot simplify down to a flat

linear function if we add the neurons

one by one we can see the simple value

functions building on one another and

the inability for one neuron to lift

itself off the x-axis doesn't seem to be

a problem many neurons working together

overcome the limitations of individual

neurons

now i manually found these weights and

biases but how would you find them

automatically the most common algorithm

for this is called back propagation and

is in fact what we're watching when we

run this program

it essentially tweaks and tunes the

parameters of the network bit by bit to

improve the approximation and the

intricacies of this algorithm are really

beyond the scope of this video i'll link

some better explanations in the

description

now we can see how this shape is formed

and why it looks like it's made up of

sort of sharp linear edges it's the

nature of the activation function we're

using

we can also see why if we use no

activation function at all the network

utterly fails to learn we need those

non-linearities

so what if we try learning a more

complicated data set like this spiral

let's give it a go

seems to be struggling a little bit to

capture the pattern no problem if we

need a more complicated function we can

add more building blocks more neurons

and layers of neurons and the network

should be able to piece together a

better approximation something that

really captures the spiral

it seems to be working

in fact no matter what the data set is

we can learn it that is because neural

networks can be rigorously proven to be

universal function approximators they

can approximate any function to any

degree of precision you could ever want

you can always add more neurons

this is essentially the whole point of

deep learning because it means that

neural networks can approximate anything

that can be expressed as a function a

system of inputs and outputs

this is an extremely general way of

thinking about the world the mandelbrot

set for instance can be written as a

function and learned all the same this

is just a scaled-up version of the

experiment we were just looking at but

with an infinitely complex data set

we don't even really need to know what

the manual brought set is the network

learns it for us and that's kind of the

point if you can express any intelligent

behavior any process any task as a

function then a network can learn it for

instance your input could be an image

and your output a label as to whether

it's a cat or a dog or your input could

be text in english and your output a

translation to spanish you just need to

be able to encode your inputs and

outputs as numbers but computers do this

all the time images video text audio

they can all be represented as numbers

and any processing you may want to do

with this data so long as you can write

it as a function can be emulated with a

neural network

it goes deeper than this though under a

few more assumptions neural networks are

provably turing complete meaning they

can solve all of the same kinds of

problems that any computer can solve

an implication of this is that any

algorithm written in any programming

language can be simulated on a neural

network but rather than being manually

written by a human it can be learned

automatically with a function

approximator

neural networks can learn anything

okay that is not true first off you

can't have an infinite number of neurons

there are practical limitations on

network size and what can be modeled in

the real world

i've also ignored the learning process

in this video and just assumed that you

can find the optimal parameters

magically how you realistically do this

introduces its own constraints on what

can be learned

additionally in order for neural

networks to approximate a function you

need the data that actually describes

that function if you don't have enough

data your approximation will be all

wrong it doesn't matter how many neurons

you have or how sophisticated your

network is you just have no idea what

your actual function should look like

it also doesn't make a lot of sense to

use a function approximator when you

already know the function you wouldn't

build a huge neural network to say learn

the mandelbrot set when you can just

write three lines of code to generate it

unless of course you want to make a cool

background visual for a youtube video

there are countless other issues that

have to be considered but for all these

complications neural networks have

proven themselves to be indispensable

for a number of really rather famously

difficult problems for computers

usually these problems require a certain

level of intuition and fuzzy logic that

computers generally lack and are very

difficult for us to manually write

programs to solve

fields like computer vision natural

language processing and other areas of

machine learning have been utterly

transformed by neural networks

and this is all because of the humble

function a simple yet powerful way to

think about the world and by combining

simple computations we can get computers

to construct any function we could ever

want

neural networks can learn almost

anything

[Music]