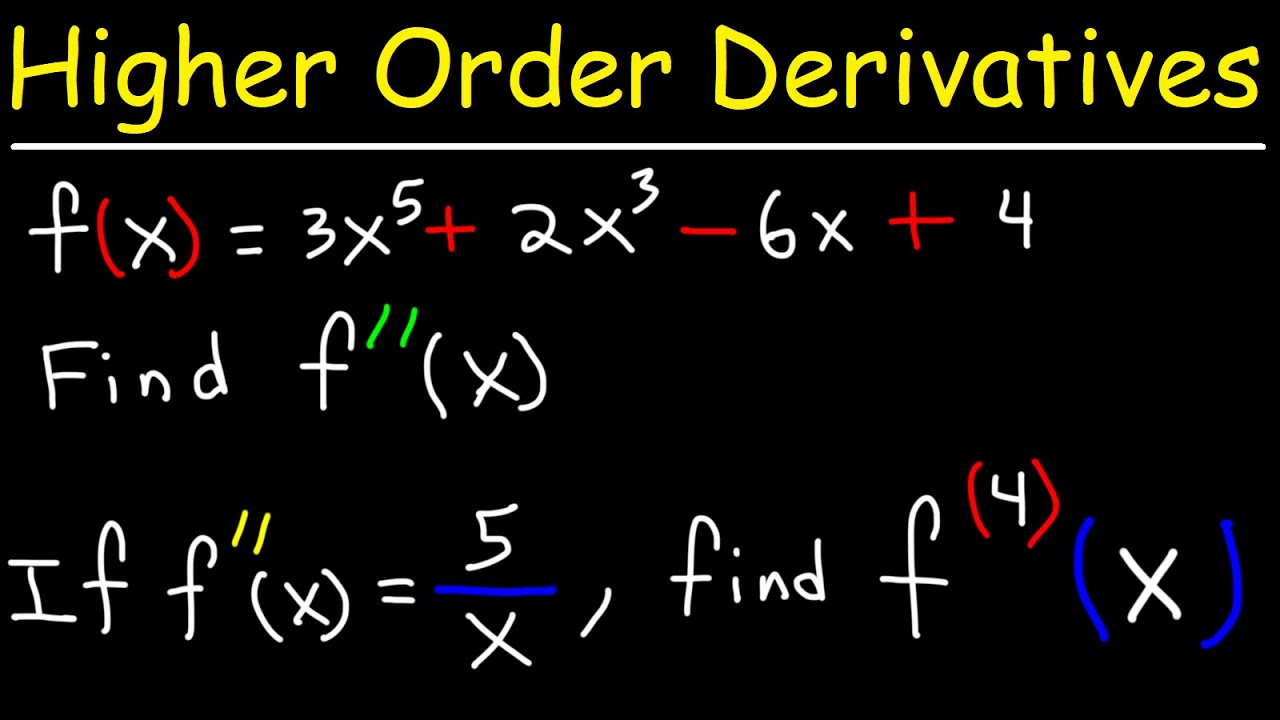
Turunan Fungsi Trigonometri 4: Turunan Kedua Fungsi Trigonometri

Summary

In this educational video, Justin Stewart Leonardo explains the process of calculating the second derivative of trigonometric functions. He starts by reviewing the first derivatives of basic trigonometric functions and shows how the same principles apply to their second derivatives. Through examples, he demonstrates the step-by-step method of deriving second derivatives using trigonometric functions like sine, cosine, tangent, and secant. The video includes a practical example of calculating the second derivative of a more complex function and concludes with exercises for the viewers to practice and verify their understanding.

Takeaways

• 😀 The video focuses on the second derivative of trigonometric functions.
• 😀 The first derivative of a trigonometric function produces another trigonometric function (e.g., if f(x) = sin(x), then f'(x) = cos(x)).
• 😀 To find the second derivative of a trigonometric function, you first need to find the first derivative.
• 😀 The second derivative of sin(x) is -sin(x), and for cos(x), it is -cos(x).
• 😀 Similar rules apply to other trigonometric functions such as tangent, cotangent, secant, and cosecant.
• 😀 The second derivative of f(x) = tan(x) is 2 * sec^2(x) * tan(x).
• 😀 The second derivative of f(x) = cot(x) is -2 * cosec^2(x) * cot(x).
• 😀 For f(x) = sec(x), the second derivative involves sec^2(x) + tan^2(x).
• 😀 The video also explains how to apply the quotient rule for differentiating complex functions, like f(x) = (x^2 + 1) / sin(x).
• 😀 A worked example is given, demonstrating how to find the second derivative using the quotient rule and simplifying the result.
• 😀 The video concludes with practice problems to help reinforce the concepts covered, including proving formulas and calculating second derivatives at specific points.

Q & A

What is the main focus of this video script?

The main focus of this video script is explaining the second derivative of trigonometric functions. It covers how to compute the second derivative of various trigonometric functions and provides examples of solving related problems.

How do you find the second derivative of a trigonometric function?

To find the second derivative of a trigonometric function, you first need to determine its first derivative. Then, apply the same derivative rules to the first derivative to calculate the second derivative.

What is the second derivative of sin(x)?

The second derivative of sin(x) is -sin(x). This is found by first taking the derivative of sin(x) to get cos(x), and then differentiating cos(x) to get -sin(x).

What is the second derivative of cos(x)?

The second derivative of cos(x) is -cos(x). This is found by first differentiating cos(x) to get -sin(x), and then differentiating -sin(x) to get -cos(x).

What is the second derivative of tan(x)?

The second derivative of tan(x) is 2 * sec^2(x) * tan(x). The first derivative of tan(x) is sec^2(x), and differentiating sec^2(x) results in the second derivative.

What formula is used to calculate the second derivative of a quotient of two functions?

To calculate the second derivative of a quotient of two functions, you use the quotient rule for derivatives. This involves taking the derivative of the numerator and denominator separately, and applying the rule twice to find the second derivative.

What is the second derivative of a function like f(x) = x^2 + 1 / sin(x)?

For the function f(x) = (x^2 + 1) / sin(x), the first derivative is computed using the quotient rule. The second derivative is then found by differentiating the first derivative again, applying rules like the product rule and chain rule.

Why is it important to first find the first derivative when computing the second derivative?

It is important to first find the first derivative because the second derivative is simply the derivative of the first derivative. Without calculating the first derivative, you cannot proceed to the second derivative.

Can the same rules for the first derivative be applied to find the second derivative?

Yes, the same rules that apply to the first derivative, such as the product rule, quotient rule, and chain rule, can also be applied when computing the second derivative.

What does the table in the video show about second derivatives of trigonometric functions?

The table in the video shows the second derivatives of several trigonometric functions. It provides quick reference for the second derivatives of functions like sin(x), cos(x), tan(x), cot(x), sec(x), and cosec(x).