Turunan Fungsi Trigonometri 2: Dalil-Dalil Turunan Fungsi Trigonometri

Summary

In this video, Justin Stewart Leonardo explains the differentiation rules for trigonometric functions, focusing on six key formulas. He demonstrates how to find the first derivatives of functions like sin(x), cos(x), tan(x), and others, using limit definitions. The video also covers rules for differentiating constants, powers, sums, differences, products, and quotients of functions. Examples are provided to illustrate each rule, making it easier to understand and apply them. Additionally, viewers are encouraged to practice with given exercises to reinforce their understanding of trigonometric derivatives.

Takeaways

• 📘 The video focuses on derivatives of trigonometric functions as outlined in section 2.2 of the lesson.
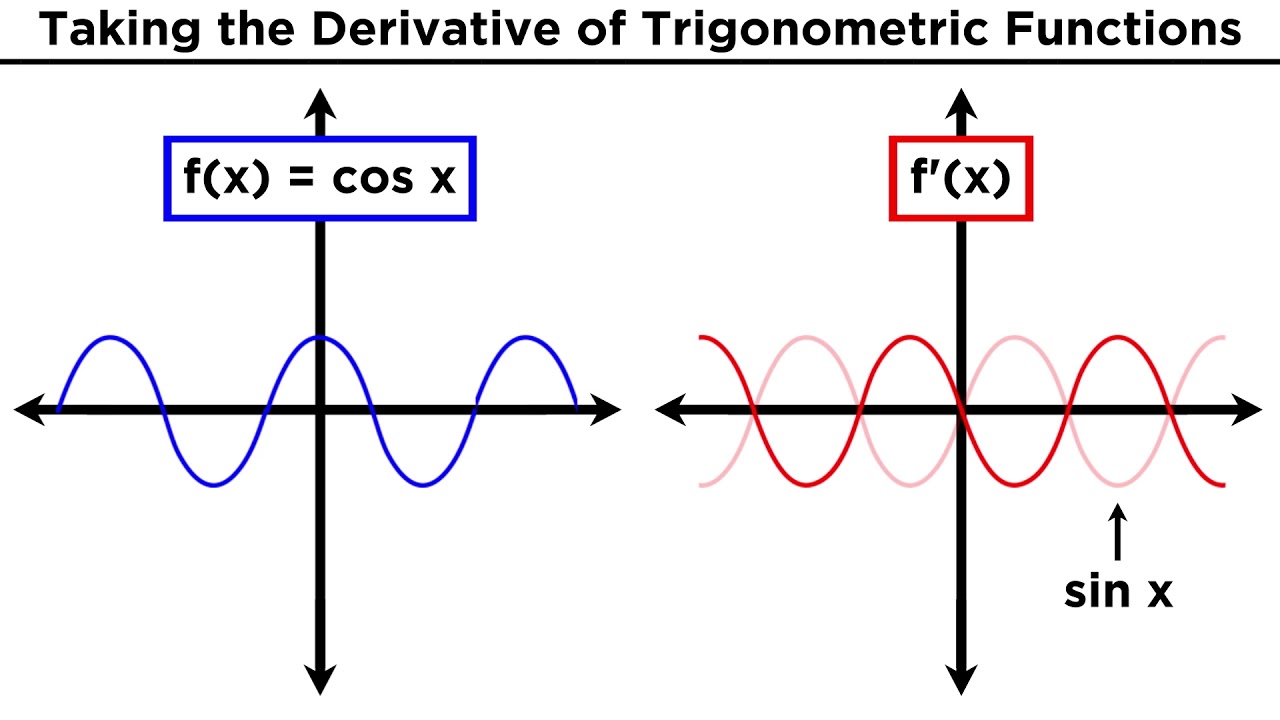
• 🔢 Six key derivative rules for trigonometric functions are explained, starting with the derivative of sin(x) being cos(x).
• 📉 Other rules include derivatives of cos(x), tan(x), cot(x), sec(x), and csc(x).
• ✍️ The derivatives are derived from the limit definition of derivatives (f(x + h) - f(x)) / h.
• 🧠 The video also covers rules for finding derivatives involving constants, powers, sums, differences, products, and quotients.
• 🧮 Example problems are given, like differentiating -2sin(x) and 7tan(x), emphasizing how to apply trigonometric derivative rules.
• 📐 The power rule is explained, with examples like differentiating sin^2(x) and cos^4(x).
• 🔄 Addition and subtraction rules for derivatives are shown, such as finding the derivative of cos(x) - 2tan^2(x) + 4x.
• ⚙️ Product rule and quotient rule are demonstrated, with examples like differentiating (x^2 - 1)cos(x) and (1 + cos(x)) / sin(x).
• 📚 The video ends with exercises for viewers to practice finding the first derivative of trigonometric functions at specific points.

Q & A

What are the six main differentiation rules for trigonometric functions discussed in the video?

The six differentiation rules for trigonometric functions are: 1. If f(x) = sin(x), then f'(x) = cos(x). 2. If f(x) = cos(x), then f'(x) = -sin(x). 3. If f(x) = tan(x), then f'(x) = sec^2(x). 4. If f(x) = cot(x), then f'(x) = -csc^2(x). 5. If f(x) = sec(x), then f'(x) = sec(x) * tan(x). 6. If f(x) = csc(x), then f'(x) = -csc(x) * cot(x).

How are the differentiation rules derived from limits?

The differentiation rules are derived using the definition of a derivative with limits. Specifically, the derivative f'(x) is calculated as the limit of (f(x + h) - f(x)) / h as h approaches zero, as mentioned in the video.

What is the differentiation rule for a function multiplied by a constant?

The differentiation rule for a function multiplied by a constant is: If h(x) = k * f(x), then h'(x) = k * f'(x), where k is a constant.

How do you differentiate a power of a trigonometric function?

To differentiate a power of a trigonometric function, use the rule: If h(x) = k * f(x)^n (where n is a positive integer and k is a constant), then h'(x) = k * n * f(x)^(n - 1) * f'(x). For example, if f(x) = sin^2(x), then f'(x) = 2 * sin(x) * cos(x).

How is the product rule for differentiation applied to trigonometric functions?

The product rule is applied as: If h(x) = f(x) * g(x), then h'(x) = f'(x) * g(x) + f(x) * g'(x). For example, if h(x) = x^2 * cos(x), then h'(x) = 2x * cos(x) - x^2 * sin(x).

What is the rule for differentiating a quotient of two functions?

The quotient rule is: If h(x) = f(x) / g(x), where g(x) ≠ 0, then h'(x) = (f'(x) * g(x) - g'(x) * f(x)) / [g(x)]^2. For example, if h(x) = (1 + cos(x)) / sin(x), then h'(x) = [-sin(x) * sin(x) - cos(x) * (1 + cos(x))] / sin^2(x).

How is the chain rule applied when differentiating a composite function?

The chain rule is applied as: If h(x) = g(f(x)), then h'(x) = g'(f(x)) * f'(x). For example, if f(x) = √cos(x), rewrite it as cos(x)^(1/2), and apply the chain rule: f'(x) = (1/2) * cos(x)^(-1/2) * (-sin(x)), giving the result f'(x) = -sin(x) / (2√cos(x)).

What happens when differentiating a sum or difference of trigonometric functions?

When differentiating a sum or difference of functions, use the rule: If h(x) = f(x) ± g(x), then h'(x) = f'(x) ± g'(x). For example, if h(x) = csc(x) - 2 * tan^2(x) + 4x, then h'(x) = -csc(x) * cot(x) - 4 * tan(x) * sec^2(x) + 4.

How do you differentiate a product of a polynomial and a trigonometric function?

To differentiate a product of a polynomial and a trigonometric function, apply the product rule: If h(x) = x^2 * cos(x), let f(x) = x^2 and g(x) = cos(x), then h'(x) = f'(x) * g(x) + f(x) * g'(x) = 2x * cos(x) - x^2 * sin(x).

How do you simplify the derivative of a trigonometric quotient?

To simplify the derivative of a trigonometric quotient, use the quotient rule and algebraic simplifications. For example, if h(x) = (1 + cos(x)) / sin(x), the derivative h'(x) simplifies to (-sin^2(x) - cos(x) * (1 + cos(x))) / sin^2(x), and further simplifies to -1 - cos(x) / sin^2(x).