Cara Menghitung Jarak Antara Dua Titik Koordinat || Teorema Pythagoras Matematika Kelas 8
Summary
TLDRThis video tutorial explains how to calculate the distance between two points on the Cartesian plane using the distance formula. It walks through multiple examples: first, finding the distance between points A (0, 4) and B (-6, 4), resulting in 6 units; then, calculating the distance between points C (1, 2) and D (4, 6), which equals 5 units. The video also demonstrates solving for an unknown coordinate, showing how to use the formula to find 'a' when given the distance and one unknown coordinate. The tutorial simplifies complex calculations, making it easy for viewers to understand and apply the distance formula.
Takeaways
- 😀 The distance between two points on a Cartesian plane can be calculated using the distance formula: √(x2 - x1)² + (y2 - y1)².
- 😀 To calculate the distance between points A(0, 4) and B(-6, 4), the distance formula yields a result of 6 units.
- 😀 The distance formula requires substituting the coordinates of the two points into the equation and simplifying the expression.
- 😀 The distance formula involves subtracting the x-coordinates and y-coordinates of the points, squaring the results, and adding them together before taking the square root.
- 😀 Squaring any negative number in the distance formula results in a positive value, ensuring that distances are always positive.
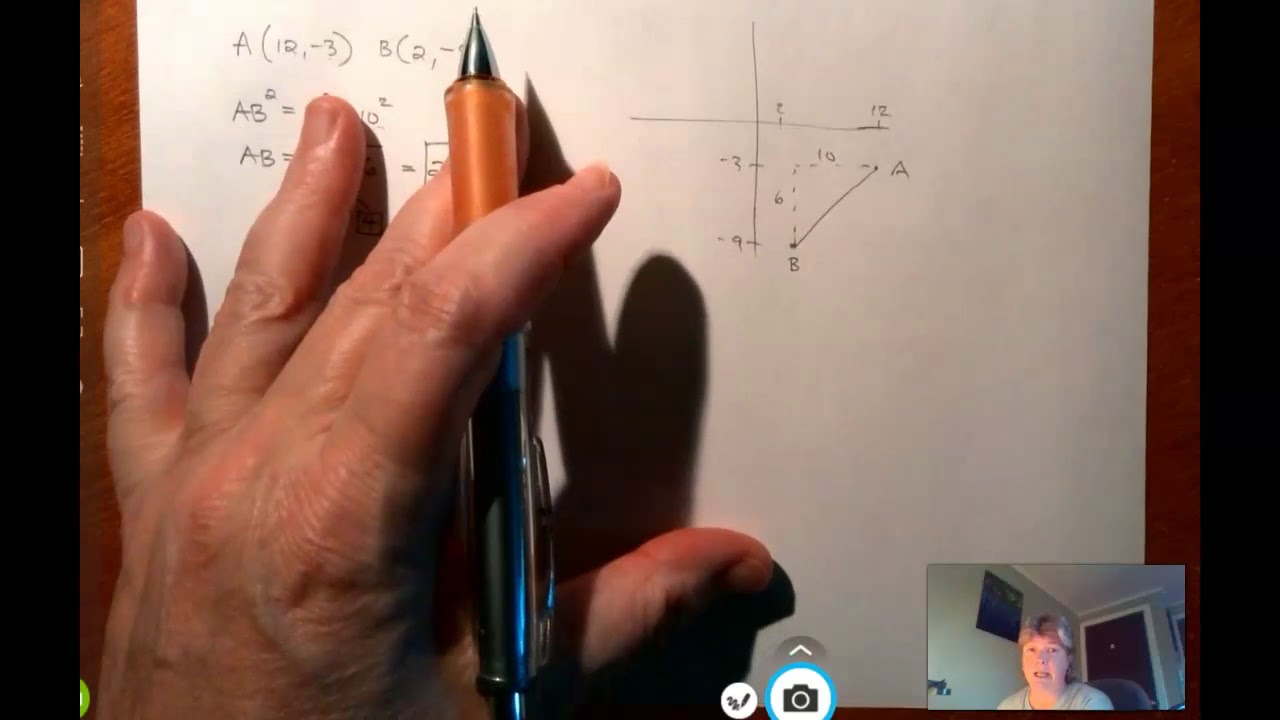
- 😀 The second problem involves finding the unknown coordinate 'a' in the point B(a, 10) given that the distance between points A(4, -5) and B is 17 units.
- 😀 To find the unknown value 'a', first apply the distance formula, then square both sides of the equation to eliminate the square root.
- 😀 After simplifying, the equation becomes (a - 4)² = 64, which leads to the possible values of 'a' being 12 and -4.
- 😀 Given that 'a' must be greater than 0, the value of 'a' is determined to be 12.
- 😀 The distance formula is a powerful tool for finding the distance between two points on a Cartesian plane, requiring knowledge of both point coordinates and basic algebra.
Q & A
What is the distance formula used to calculate the distance between two points on the Cartesian plane?
-The distance formula is: d = √[(x2 - x1)² + (y2 - y1)²], where (x1, y1) and (x2, y2) are the coordinates of the two points.
What is the first example in the transcript for calculating the distance between two points?
-The first example involves calculating the distance between points A(0, 4) and B(-6, 4) using the distance formula.
What are the steps to calculate the distance between points A(0, 4) and B(-6, 4)?
-1. Subtract the x-coordinates: -6 - 0 = -6. 2. Subtract the y-coordinates: 4 - 4 = 0. 3. Square the results: (-6)² = 36, 0² = 0. 4. Add the squares: 36 + 0 = 36. 5. Take the square root: √36 = 6.
What is the final result for the distance between points A(0, 4) and B(-6, 4)?
-The distance between points A and B is 6 units.
How does the second example in the transcript differ from the first example?
-In the second example, the distance between two points is given, but one of the coordinates is unknown (point B is B(a, 10)), and we are asked to find the unknown value 'a'.
How is the distance formula applied to find the unknown value 'a' in the second example?
-We set up the equation using the distance formula: 17 = √[(a - 4)² + (10 - (-5))²]. Then we solve for 'a' by simplifying the equation and isolating 'a'.
What is the value of 'a' after solving the second example?
-The value of 'a' is found to be 12 after solving the equation.
What is the importance of understanding the distance formula in geometry?
-The distance formula is essential for calculating the distance between any two points on the Cartesian plane, which is a foundational concept in geometry, useful in various applications such as physics, engineering, and computer science.
What happens when the distance formula involves subtracting a negative number in the second example?
-When subtracting a negative number, it becomes addition. For example, 10 - (-5) becomes 10 + 5, resulting in 15.
Why is it important to square the differences in the distance formula?
-Squaring the differences ensures that the result is always positive, allowing us to calculate the actual distance between points, regardless of their direction on the plane.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Distance Formula | Introduction to Analytic Geometry|

APPLYING DISTANCE FORMULA TO PROVE GEOMETRIC PROPERTIES

Como calcular la DISTANCIA entre dos puntos en el PLANO CARTESIANO. Usando el Teorema de Pitagoras.
Distance and Midpoint

Pensamiento Matemático II PROGRESION 11

How to find Euclidean Manhattan Minkowski distance Supremum distance Cosine Similarity Mahesh Huddar
5.0 / 5 (0 votes)