AREA ENTRE CURVAS EJEM1
Summary
TLDREn este video, se explica cómo calcular el área entre dos funciones usando una integral definida. El instructor aborda desde el inicio la importancia de graficar las funciones para entender mejor los puntos de intersección. Se resuelve un ejemplo paso a paso, igualando las funciones p(x) = x^2 + 1 y q(x) = 2x + 1, determinando los límites de integración y evaluando la integral resultante. El video destaca también cómo identificar qué función está arriba de la otra y ofrece una demostración en Geogebra para confirmar el cálculo del área, que resulta ser 1.33 unidades cuadradas.
Takeaways
- ✏️ La fórmula para determinar el área entre dos funciones es la integral definida desde 'a' hasta 'b' de (f(x) - g(x)) dx.
- 📊 Es útil graficar las funciones primero para visualizar dónde se cruzan y facilitar la resolución.
- 📝 El primer paso es igualar las funciones para encontrar los puntos de cruce.
- ➗ Al resolver la ecuación obtenida al igualar las funciones, se determinan los límites de integración.
- 📉 La función que esté más arriba en el intervalo de integración es la que se resta primero en la integral.
- 🔎 Si no se tiene la gráfica, se puede evaluar las funciones en un punto dentro del intervalo para ver cuál está más arriba.
- ➕ Después de establecer la integral, se realizan las operaciones algebraicas antes de integrar.
- 🧮 La integral se calcula separadamente para cada término, resolviendo luego con los límites de integración.
- ✅ Una vez integrada la función, se evalúa el resultado en los límites superior e inferior y se resta.
- 🔢 El área entre las curvas es 4/3 unidades cuadradas, lo que equivale a aproximadamente 1.33.
Q & A
¿Cuál es el primer paso para resolver el área entre dos curvas?
-El primer paso es igualar las funciones para determinar los puntos donde se cruzan, lo que ayudará a establecer los límites de integración.
¿Qué importancia tiene graficar las funciones antes de resolver la integral?
-Graficar las funciones permite visualizar los puntos de cruce y la disposición de las curvas, facilitando la identificación de cuál está más arriba y, por lo tanto, cuál será la función 'f(x)' en la integral.
¿Qué significa igualar las funciones?
-Igualar las funciones implica poner las dos funciones en igualdad (p(x) = q(x)) y luego resolver la ecuación resultante para encontrar los puntos de cruce, que determinan los límites de integración.
¿Cómo se determina cuál función va primero en la integral?
-La función que va primero en la integral es la que está más arriba en el intervalo de integración. Esto se puede verificar evaluando ambas funciones en un punto intermedio del intervalo.
¿Cómo se simplifica la ecuación cuadrática resultante al igualar las funciones?
-Al igualar las funciones, se pasa todo al mismo lado de la ecuación, simplificando los términos comunes. En este caso, se obtiene una ecuación cuadrática que puede resolverse por factorización.
¿Qué sucede si no tienes una gráfica de las funciones?
-Si no tienes una gráfica, puedes evaluar ambas funciones en un punto intermedio del intervalo de integración para determinar cuál función está más arriba.
¿Cómo se estructuran las integrales cuando hay más de un término?
-Cuando hay más de un término, se pueden dividir las integrales en varias, una por cada término, y luego resolverlas individualmente antes de sumar los resultados.
¿Por qué el proceso de integración no es el paso más complicado en este tipo de problemas?
-El verdadero reto suele estar en resolver la ecuación resultante del primer paso (igualar las funciones), ya que puede implicar ecuaciones de mayor grado. La integración en sí, a menudo, es más directa.
¿Qué es importante recordar cuando evalúas una integral definida?
-Es importante recordar que debes evaluar el resultado de la integral en los límites superior e inferior, y luego restar para obtener el área.
¿Cómo verificas si el área calculada es correcta?
-Puedes verificar el área utilizando una herramienta gráfica como GeoGebra, donde puedes ingresar las funciones y los límites para que el software calcule automáticamente el área entre las curvas.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
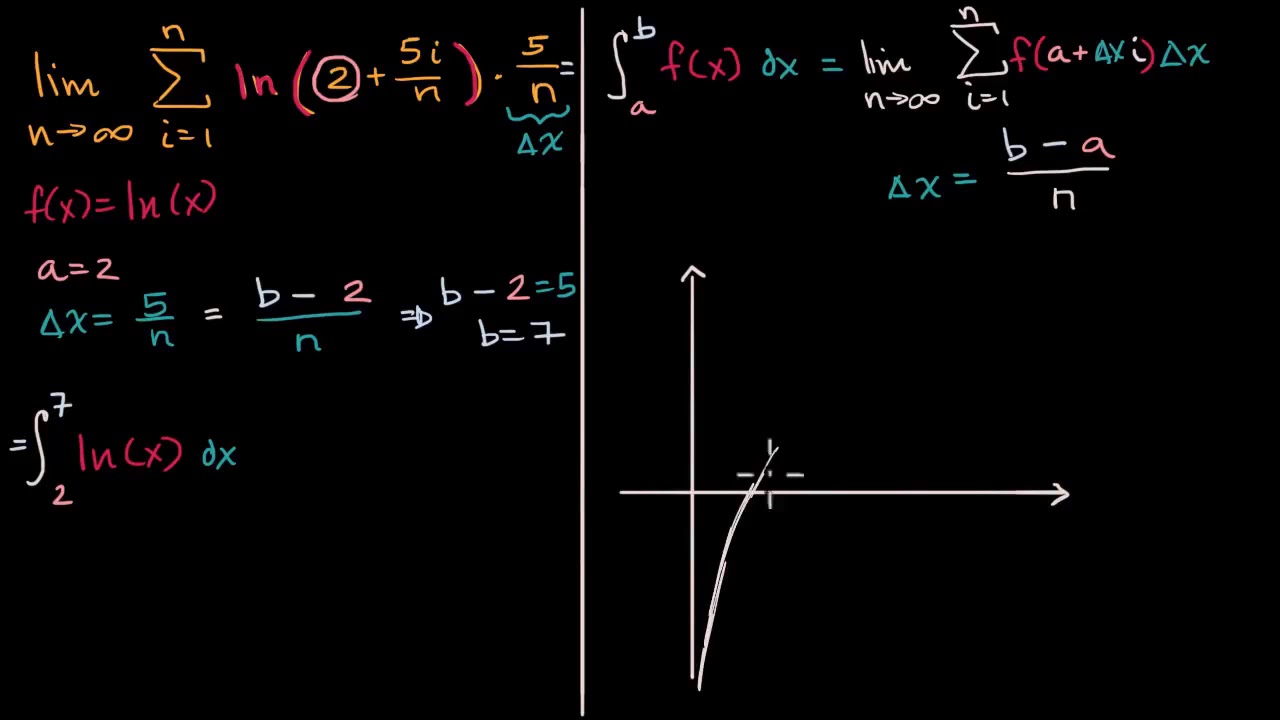
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español

AREA ENTRE CURVAS INTRO

Reescribir una integral definida como el límite de una suma de Riemann | Khan Academy en Español

Análisis Matemático II - Teorema Fundamental de Cálculo Integral - Parte 3

Introducción al cálculo integral | Khan Academy en Español

AREA ENTRE CURVAS EJEM2
5.0 / 5 (0 votes)
