Calcular la PROBABILIDAD de una DISTRIBUCIÓN NORMAL - problema 1
Summary
TLDREl profesor Jose Andalón presenta un tutorial sobre cómo calcular la probabilidad de datos en una distribución normal dada la media y la desviación estándar. Destaca la importancia de entender la distribución normal, también conocida como 'forma de campana', y cómo la desviación estándar indica la dispersión de los datos en relación con la media. Utiliza un ejemplo práctico de las temperaturas de una ciudad en octubre, con una media de 19.3 grados Celsius y una desviación estándar de 4 grados Celsius, para ilustrar cómo calcular la probabilidad de tener una temperatura menor o igual a 22 grados Celsius. El profesor explica el proceso de conversión a un valor z y cómo utilizar tablas de distribución normal para encontrar la probabilidad. Además, recomienda el uso de una calculadora Casio FX-50 para facilitar los cálculos y comprobar los resultados. Finalmente, ofrece un resumen de cómo obtener la probabilidad exacta y cómo ajustar los parámetros para diferentes intervalos de temperatura, subrayando el valor de la herramienta gráfica para una comprensión más profunda del problema.
Takeaways
- 📚 El profesor Jose Andalón explica cómo calcular la probabilidad de datos con una distribución normal dada la media y la desviación estándar.
- 📊 La desviación estándar indica la dispersión de los datos en relación a la media, ayudando a entender qué tan alejados están los valores.
- 🌡️ Se utiliza un ejemplo de temperaturas de una ciudad en octubre, con una media de 19.3 grados Celsius y una desviación estándar de 4 grados Celsius.
- 🔢 Para calcular la probabilidad de una temperatura específica (menor o igual a 22 grados Celsius), se realiza una conversión en un valor z.
- ➗ El valor z se calcula restando la media y dividiendo entre la desviación estándar, lo que en este caso sería (22 - 19.3) / 4.
- 📈 La probabilidad total bajo la curva de una distribución normal es 1, y la mitad de esa área (0.5) corresponde a la media.
- 📉 El valor z se utiliza para encontrar la probabilidad en una tabla de distribución normal, que puede ser de izquierda a derecha o de derecha a izquierda.
- 🔍 Se recomienda trabajar con una tabla que comience en 0.5 y aumente hasta 1 para facilitar la comprensión de la probabilidad.
- 🧮 La probabilidad aproximada para una temperatura menor o igual a 22 grados Celsius se encuentra entre 0.7486 y 0.7517.
- 📊 Para verificar el resultado, se puede usar una calculadora gráfica como la Casio fx-CG 50, que permite hacer cálculos estadísticos y visualizar la distribución normal.
- 🌡️ El ejemplo muestra cómo cambiar los parámetros en la calculadora para encontrar la probabilidad de temperaturas específicas, como menor o igual a 15 grados Celsius.
Q & A
¿Quién es el profesor que aparece en el video?
-El profesor que aparece en el video es el profesor José Andalón.
¿Qué tema trata de explicar el profesor en el video?
-El profesor trata de explicar cómo calcular la probabilidad de datos cuando se conoce la media y la desviación estándar, y los datos siguen una distribución normal.
¿Por qué es importante calcular la probabilidad de un evento?
-Calcular la probabilidad de un evento es importante porque nos permite saber si un evento va a ocurrir o no, lo que puede ser útil en la toma de decisiones y en la predicción de resultados.
¿Qué herramienta utiliza el profesor para facilitar el cálculo de la probabilidad?
-El profesor utiliza una calculadora Casio FX para facilitar el cálculo de la probabilidad, ya que permite mover el intervalo de la probabilidad en la distribución normal sin tener que hacer todo el procedimiento de análisis a mano.
¿Cómo se interpreta la desviación estándar en el contexto de una distribución de datos?
-La desviación estándar indica qué tan dispersos o separados se encuentran los datos con respecto a la media. Un valor grande de desviación estándar sugiere que los datos están más dispersos, mientras que un valor pequeño sugiere que están más集中 (concentrados).
¿Cuál es el promedio y la desviación estándar de las temperaturas mencionadas en el ejemplo del video?
-El promedio de las temperaturas mencionadas en el ejemplo es de 19.3 grados Celsius y la desviación estándar es de 4 grados Celsius.
¿Cómo se calcula la probabilidad de que la temperatura sea menor o igual a 22 grados Celsius?
-Para calcular la probabilidad, se realiza una conversión en z, donde z es igual a (valor de interés - media) / desviación estándar. Luego, se utiliza una tabla de distribución normal o una calculadora para encontrar la probabilidad asociada a ese valor z.
¿Qué es una 'campana' en el contexto de una distribución de datos?
-Una 'campana' es una forma de describir la distribución normal de los datos, donde la mayoría de los datos se concentran alrededor de la media, y la frecuencia disminuye a medida que se alejan de la media.
¿Cómo se interpreta el valor z en el campo de las distribuciones normales?
-En el campo de las distribuciones normales, un valor z de 0 representa la media. Un valor z positivo indica que el dato está desviado en la dirección positiva de la media, mientras que un valor z negativo indica una desviación en la dirección negativa.
¿Cómo se utiliza la tabla de distribución normal para encontrar la probabilidad de un evento?
-Se busca el valor z correspondiente en la tabla de distribución normal y se lee la probabilidad directamente. La tabla muestra la probabilidad acumulada a la derecha del valor z, por lo que se utiliza para encontrar la probabilidad de eventos que ocurren por encima de un cierto umbral.
¿Cómo se utiliza la calculadora gráfica Dora para verificar el resultado de la probabilidad?
-Se utiliza la calculadora gráfica Dora para ingresar los parámetros de la distribución normal (media, desviación estándar) y el intervalo de interés. Luego, se utiliza la función de distribución acumulada para obtener la probabilidad del intervalo especificado.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
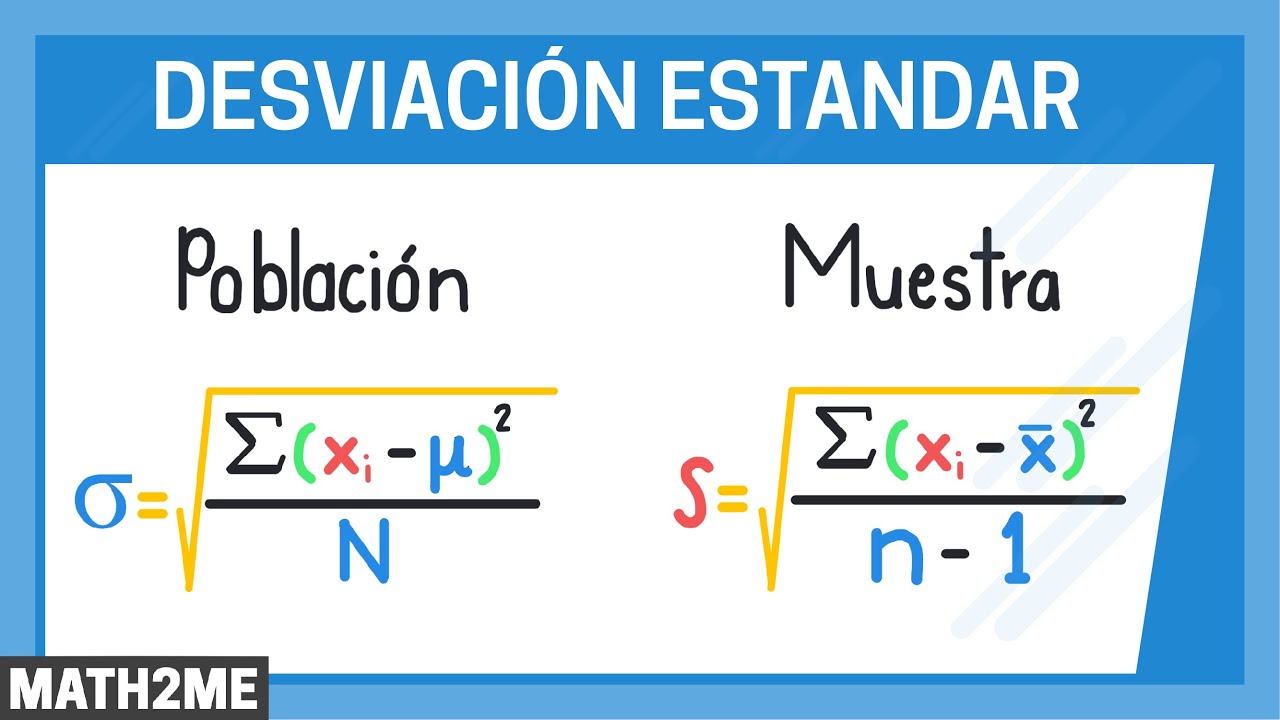
Desviación estándar en una población y muestra | Introdución | Fx-991EX

¿Qué es la Distribución Normal? | Videos Educativos Aula365

DISTRIBUIÇÃO NORMAL ESTATÍSTICA

Distribución normal ejemplo

Estandarización de una variable con distribución normal
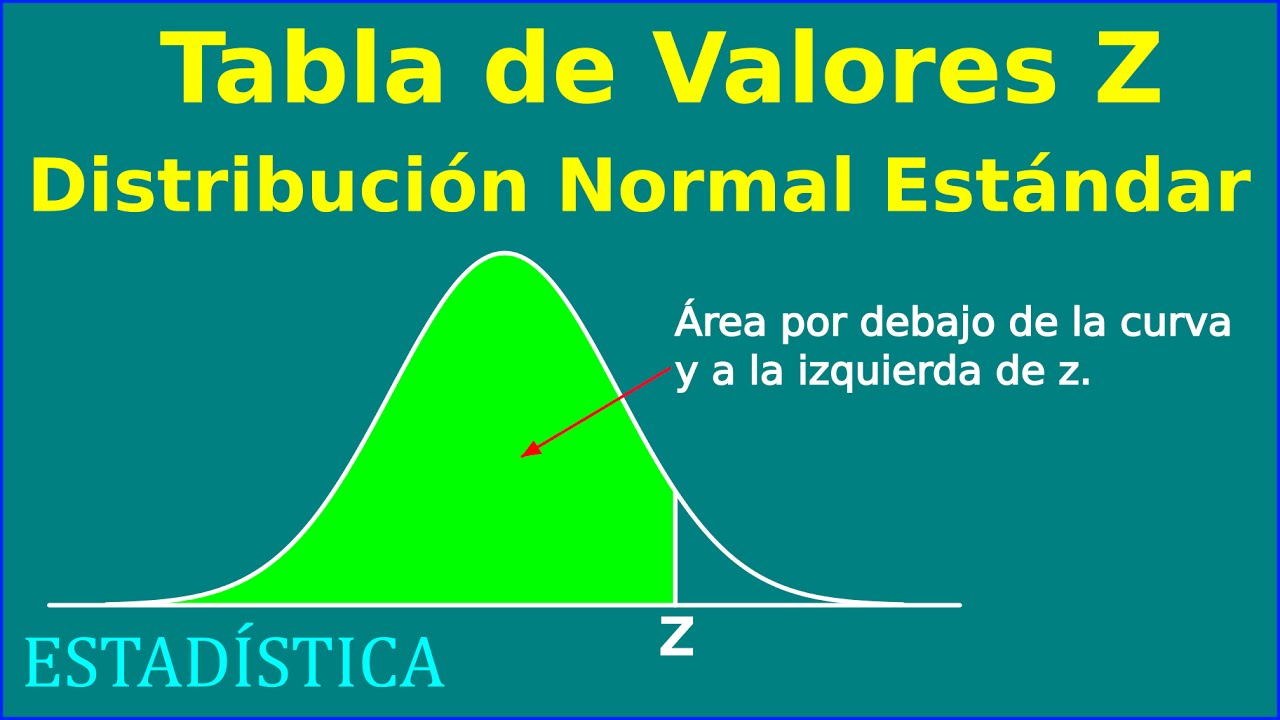
Tabla de probabilidades de la Distribucion Normal Estandar - Valores z
5.0 / 5 (0 votes)
