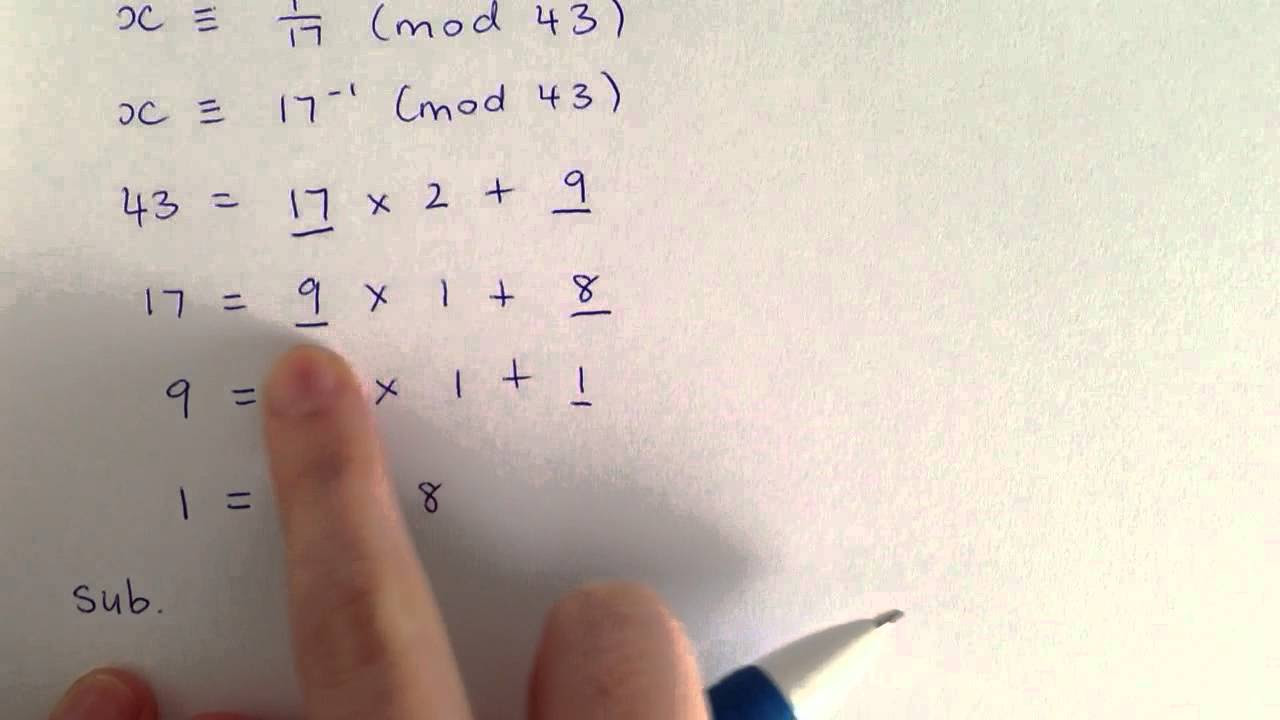Contracting the Extended Euclidean Algorithm (Proof)

Summary

In this video, the speaker presents a proof of the Extended Euclidean Algorithm, detailing how to express the greatest common divisor (gcd) of two integers as a linear combination of their remainders. The proof begins with a clear notation system, making complex expressions more manageable. Using a recursive approach, the speaker establishes a theorem that connects the remainders with specific coefficients. The proof is structured inductively, confirming its validity for various cases. This exploration not only clarifies the algorithm's workings but also demonstrates the effectiveness of the proposed graphical organizer for simplifying calculations.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.