Aplicación Segunda Ley (Solución del Sistema de Ecuaciones)
Summary
TLDREn este video, se aborda un sistema de ecuaciones derivado de fuerzas en un escenario físico, donde se analizan las componentes de fuerzas como la tensión, la gravedad y la fricción. Se explica cómo establecer y resolver ecuaciones relacionadas con las fuerzas en cuerpos en movimiento, incluyendo el concepto de fricción cinética y su relación empírica con la normal. El objetivo es encontrar los valores de las variables relevantes, como la tensión en la cuerda y la fuerza de fricción, utilizando datos conocidos como masas y coeficientes de fricción. Finalmente, se detalla el proceso de simplificación y resolución del sistema de ecuaciones.
Takeaways
- 😀 Se introduce un sistema de ecuaciones derivado de ecuaciones vectoriales relacionadas con fuerzas en dos masas.
- 💡 La primera componente del sistema incluye la tensión en la cuerda (T), la fuerza gravitacional (mg) y la aceleración (a).
- 🔄 Las segundas componentes están relacionadas con las fuerzas en la masa colgante, incluyendo tensión y fuerza gravitacional.
- 📊 Se obtienen tres ecuaciones principales y una cuarta ecuación empírica relacionada con la fricción cinética.
- ⚖️ La fricción cinética se describe como proporcional a la fuerza normal, definiendo así el coeficiente de fricción cinética.
- 🧮 Los datos conocidos incluyen las masas de los cuerpos, el coeficiente de fricción cinética y la gravedad.
- 🔍 El objetivo es determinar los valores de la tensión, la fuerza de fricción y la fuerza normal.
- ✂️ Se realiza una sustitución para expresar la fuerza normal como equivalente al peso del objeto (mg).
- 🧩 Se describe un método para restar ecuaciones y aislar variables como la tensión (T) y la aceleración (a).
- ✅ Al final, se obtienen los valores de aceleración, fuerza normal y tensión a través de simplificación y sustitución.
Q & A
¿Cuál es el sistema de ecuaciones mencionado en la transcripción?
-El sistema de ecuaciones se deriva de las ecuaciones vectoriales que describen las fuerzas actuantes en dos masas conectadas por una cuerda.
¿Qué componentes se consideran en las ecuaciones vectoriales?
-Se consideran las componentes a lo largo de los ejes x e y, donde se analiza la tensión en la cuerda y las fuerzas como el peso y la fuerza de rozamiento.
¿Qué representa la fuerza de rozamiento cinética en el contexto de la transcripción?
-La fuerza de rozamiento cinética se refiere a la fuerza que se opone al deslizamiento entre dos superficies y es proporcional a la normal entre ellas.
¿Cómo se determina la fuerza de rozamiento cinética?
-Se determina empíricamente y se expresa como el producto del coeficiente de rozamiento cinético y la fuerza normal.
¿Qué datos se conocen al resolver el sistema de ecuaciones?
-Se conocen las masas de los cuerpos, el coeficiente de rozamiento cinético y la aceleración debida a la gravedad.
¿Cómo se relaciona la normal con el peso en el contexto de este problema?
-La fuerza normal es igual al peso del cuerpo que actúa perpendicularmente a la superficie.
¿Qué método se utiliza para resolver el sistema de ecuaciones?
-Se utilizan métodos algebraicos, como restar ecuaciones y sustituir valores conocidos, para despejar las incógnitas.
¿Qué se obtiene al despejar la tensión en la cuerda?
-Se obtiene la magnitud de la fuerza que ejerce la cuerda sobre el cuerpo, que se relaciona con la aceleración y las fuerzas que actúan sobre el sistema.
¿Por qué es importante la factorización en la resolución del sistema de ecuaciones?
-La factorización simplifica las ecuaciones, facilitando el despeje de variables y la obtención de resultados más claros.
¿Cuál es el resultado final de resolver el sistema de ecuaciones?
-Se obtiene el valor de la aceleración del sistema, la magnitud de la fuerza de rozamiento y la tensión en la cuerda en términos de los datos conocidos.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Tensión en un sistema con aceleración y pastelazo en el rostro | Física | Khan Academy en Español

EJERCICIO - LEYES DE NEWTON: TRES BLOQUES UNIDOS POR CUERDAS
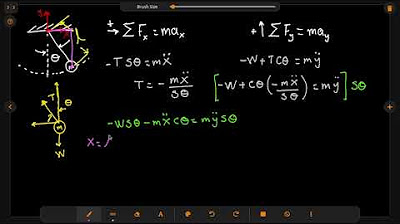
Modelado matemático de péndulo simple

FUERZAS que ACTÚAN sobre un CUERPO 🏋️♂️

Plano inclinado con rozamiento - 2da ley de Newton

Inverted Pendulum, 10/2/2016
5.0 / 5 (0 votes)
