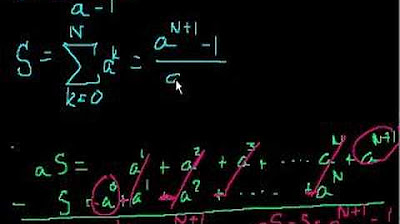Convergence and Divergence - Introduction to Series

Summary

This video explains how to determine if an infinite series converges or diverges using the sequence defined by aₙ = 2n as an example. It clarifies the difference between sequences and series, introducing concepts like partial sums and the divergence test. The speaker demonstrates how to find the limit of partial sums to establish convergence, illustrating that if the limit equals infinity, the series diverges. Additionally, it discusses the significance of the divergence test, where a non-zero limit indicates divergence, while a zero limit requires further testing. Ultimately, it emphasizes understanding these principles for evaluating infinite series.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.