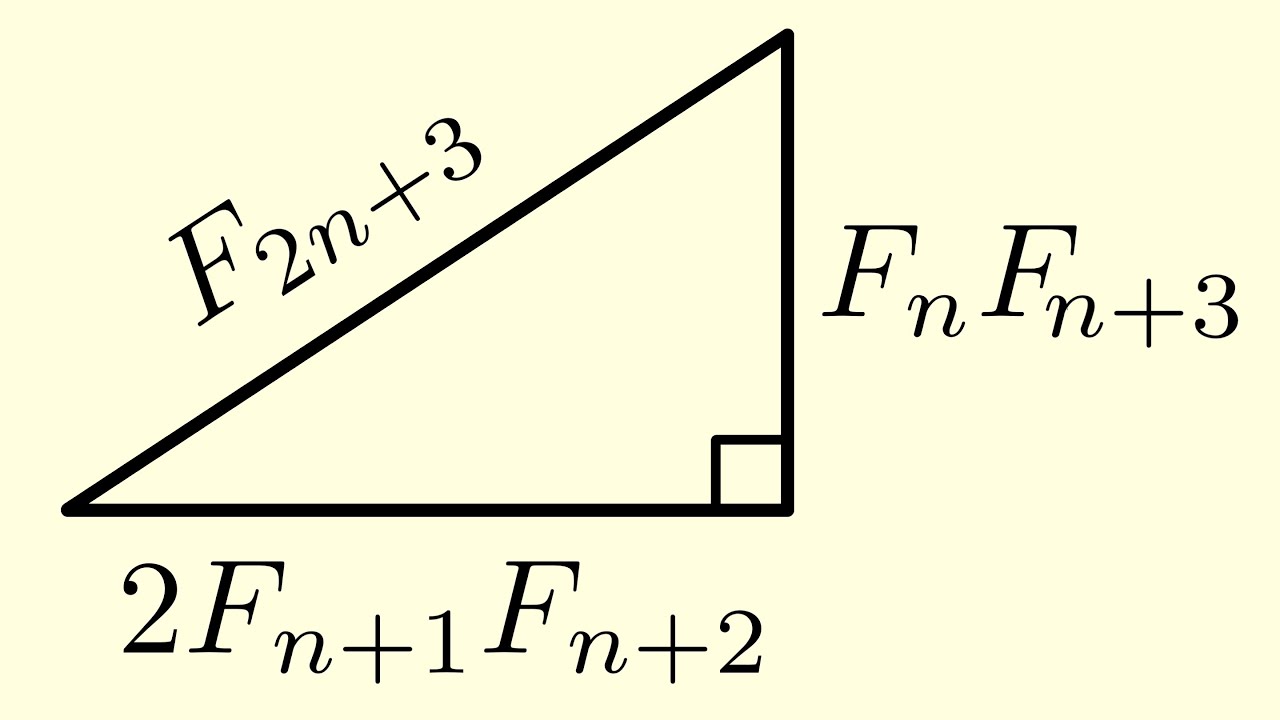One second to compute the largest Fibonacci number I can

Summary

This video delves into the fascinating world of Fibonacci numbers and their mathematical properties. It explores efficient methods for calculating high powers of the Fibonacci transition matrix using diagonalization and Binet's formula, which expresses Fibonacci numbers through irrational numbers. The speaker introduces computational strategies, particularly Fast Fourier Transform (FFT), to optimize calculations, allowing for the determination of Fibonacci numbers beyond the 4 millionth in under a second. The video balances technical insights with philosophical reflections on content engagement, inviting viewers to appreciate both the beauty of mathematics and the nature of learning.

Takeaways

• 😀 High powers of a 2x2 matrix are challenging to calculate by hand but can be simplified with diagonal matrices.
• 😀 The Fibonacci transition matrix is not diagonal but is diagonalisable, allowing for easier computation of Fibonacci numbers.
• 😀 Binet's formula provides a closed-form expression for the nth Fibonacci number, utilizing irrational numbers derived from the golden ratio.
• 😀 Fibonacci numbers can be approximated using the expression (-phi)^(-n), which converges quickly to zero.
• 😀 The nth Fibonacci number can be computed by evaluating (1 + √5)^n, extracting coefficients, and adjusting by dividing with 2^n.
• 😀 Implementing Fibonacci calculations can be optimized by using a Z[√5] structure to represent numbers as pairs, enhancing memory efficiency.
• 😀 The algorithm operates in O(n log n) time complexity when using Fast Fourier Transforms (FFTs) for multiplication.
• 😀 Limitations exist when using FFTs, particularly regarding the precision of large number multiplications.
• 😀 The required precision for FFTs increases with the size of the numbers, necessitating careful management to avoid inaccuracies.
• 😀 The speaker emphasizes the human aspect of content consumption, acknowledging that viewer preferences may vary.

Q & A

What is the primary mathematical challenge addressed in the video?

The video focuses on calculating high powers of a 2x2 matrix, which can be complex and computationally intensive.

Why are small powers of a general 2x2 matrix considered impractical to compute by hand?

Even small powers of a general 2x2 matrix involve tedious calculations that are best handled by a computer due to their complexity.

How does the video define a diagonal matrix, and why is it significant?

A diagonal matrix is a matrix where non-diagonal elements are zero. It is significant because high powers of diagonal matrices can be computed easily, making calculations more manageable.

What is Binet's formula, and how does it relate to Fibonacci numbers?

Binet's formula provides a closed formula for calculating the nth Fibonacci number using the golden ratio. It derives from the diagonalization of the Fibonacci transition matrix.

Why are irrational numbers mentioned as a limitation for computational efficiency?

Irrational numbers can be challenging for computers to handle efficiently. The video emphasizes using specific real numbers, particularly those formed by rational numbers and root five, to maintain computational efficiency.

What technique is suggested to improve the calculation of Fibonacci numbers?

The video suggests using pairs of numbers to represent elements of Z[√5], which can optimize the implementation of Binet's formula and improve performance.

What is the significance of the complexity class O(n log n) mentioned in the video?

O(n log n) indicates the algorithm's time complexity when using Fast Fourier Transforms (FFTs) for multiplication, which is efficient compared to other methods.

How does the video explain the potential for error in Fast Fourier Transforms?

The video details how the precision requirements for Fourier transforms can lead to errors, particularly when multiplying large numbers. It emphasizes the importance of maintaining enough bits of precision during computations.

What insights does the video provide about the limitations of FFT algorithms?

The video reveals that while FFT algorithms can handle large numbers, they have limitations, particularly as Fibonacci numbers approach a size that exceeds the memory limits of the algorithms.

What life lesson does the presenter convey at the end of the video?

The presenter emphasizes the importance of skepticism regarding online content, highlighting that not everything seen on the internet can be trusted, even in mathematical or computational contexts.