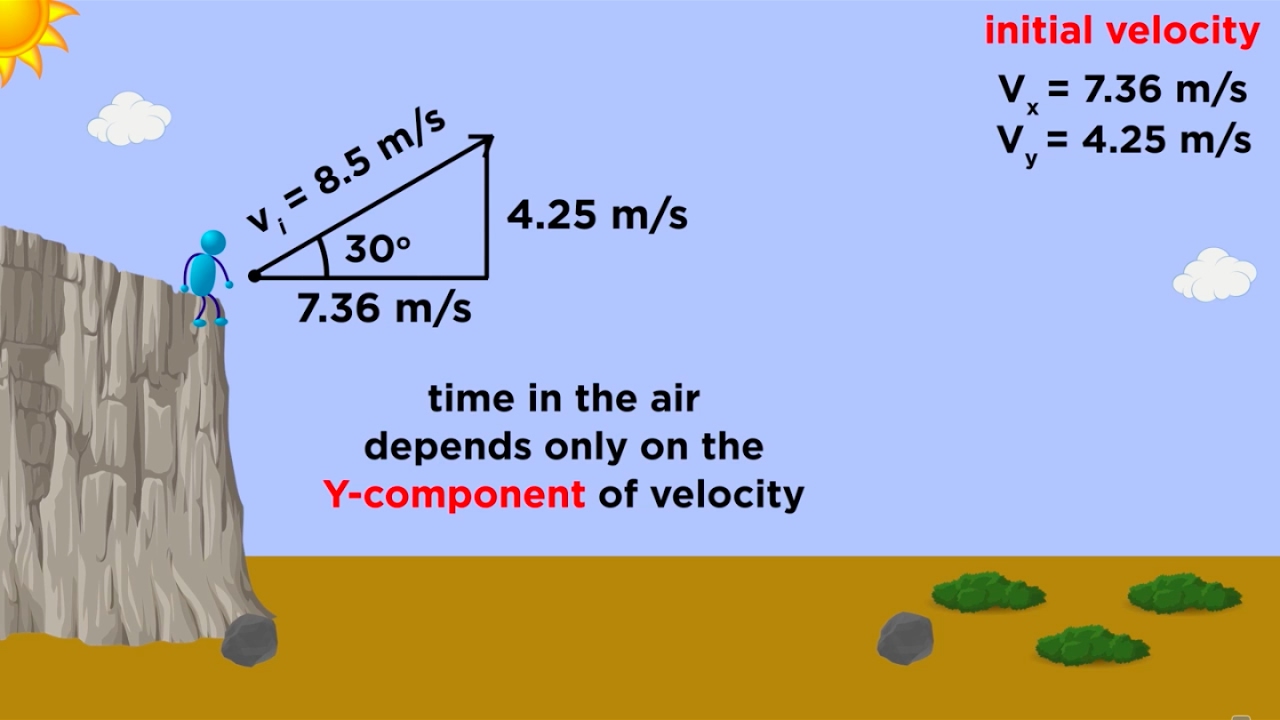
A student stands at the edge of a cliff and throws a stone horizontally
Summary
TLDRThis video tutorial delves into the physics of projectile motion, guiding viewers through a problem involving a stone thrown horizontally from a cliff. It outlines the process of determining the stone's initial coordinates, velocity components, and equations of motion. Key calculations include the time of flight, impact speed, and angle upon hitting the ground. The final results reveal that the stone impacts the beach approximately 3.19 seconds later, with a speed of about 36.1 m/s at an angle of 60.1 degrees below the horizontal. This comprehensive breakdown enhances understanding of kinematics in a practical context.
Takeaways
- 😀 The initial position of the stone is at coordinates (0 m, 50 m).
- 📏 The stone is thrown horizontally with an initial velocity of 18 m/s in the x-direction.
- 🚫 The initial velocity in the y-direction is 0 m/s since the stone is not moving vertically when released.
- ⚖️ In projectile motion, the x-direction acceleration is always 0 m/s², simplifying calculations.
- 📐 The equation for the x-component of the velocity remains constant at 18 m/s.
- 🌌 The y-component of velocity is influenced by gravity, with an acceleration of 9.8 m/s².
- 🕒 To find the time of flight until the stone hits the beach, the final y position is set to 0 m.
- ⏱️ The calculated time for the stone to strike the beach is approximately 3.19 seconds.
- 💨 The final speed at impact is 36.1 m/s, derived using the Pythagorean theorem.
- 📏 The impact angle of the stone is 60.1° below the horizontal.
Q & A
What are the initial coordinates of the stone before it is thrown?
-The initial coordinates of the stone are (0 m, 50 m), where 50 m represents the height of the cliff.
What is the initial velocity of the stone in the X direction?
-The initial velocity in the X direction is +18 m/s, indicating that the stone is thrown horizontally.
What is the initial velocity of the stone in the Y direction?
-The initial velocity in the Y direction is 0 m/s because the stone is not moving vertically at the moment of being thrown.
How does the acceleration affect the stone's motion in the X direction?
-In the X direction, the acceleration is 0 m/s², which means there is no change in velocity, and the stone maintains a constant velocity of 18 m/s.
What is the equation for the Y component of the stone's velocity?
-The equation for the Y component of the velocity is v_y = v_{0y} + a_y * t, where a_y is the acceleration due to gravity (9.8 m/s²).
What are the equations of motion used to describe the stone's position over time?
-The equations are: x(t) = 18t for the X position and y(t) = 50 - 4.9t² for the Y position.
How long does it take for the stone to strike the beach below the cliff?
-The stone strikes the beach approximately 3.19 seconds after being released.
What is the final speed of the stone just before it impacts the beach?
-The final speed of the stone at impact is approximately 36.1 m/s.
What angle does the stone make with the horizontal at the point of impact?
-The angle below the horizontal at the point of impact is approximately 60.1 degrees.
How is the resultant velocity of the stone calculated at impact?
-The resultant velocity is calculated using the Pythagorean theorem, combining the X and Y components of velocity.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
5.0 / 5 (0 votes)